
已知向量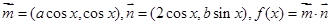 且
且
(1)若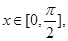 ,求
,求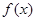 的最大值与最小值
的最大值与最小值
(2)若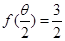 ,且
,且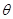 是三角形的一个内角,求
是三角形的一个内角,求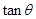
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
设函数f(x)=  ×
× ,其中向量
,其中向量 ="(2cosx,1),"
="(2cosx,1),"  =(cosx,
=(cosx, sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间;
(2)当xÎ[0, ]时,ô f(x)ô <4恒成立,求实数m的取值范围.
]时,ô f(x)ô <4恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数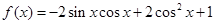
(1)设方程 在(0,
在(0,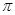 )内有两个零点
)内有两个零点 ,求
,求 的值;
的值;
(2)若把函数 的图像向左移动
的图像向左移动
 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于 轴对称,求
轴对称,求 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在半径为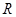 、圆心角为
、圆心角为 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形 ,并且
,并且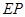 与
与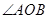 的平分线
的平分线 平行,设
平行,设 .
.
(1)试写出用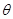 表示长方形
表示长方形 的面积
的面积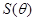 的函数;
的函数;
(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形 的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com