
| A. | 向左平移$\frac{1}{2}$个周期 | B. | 向右平移$\frac{1}{2}$个周期 | ||
| C. | 向左平移$\frac{1}{4}$个周期 | D. | 向右平移$\frac{1}{4}$个周期 |
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x∈R,使得x3-x2+1<0 | B. | 存在x∈R,使得x3-x2+1<0 | ||
| C. | 对任意的x∈R,都有x3-x2+1≥0 | D. | 存在x∈R,使得x3-x2+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
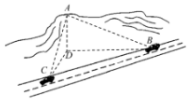 如图,小明同学在山顶A处观测到,一辆汽车在一条水平的公路上沿直线匀速行驶,小明在A处测得公路上B,C两点的俯角分别为30°,45°,且∠BAC=135°.若山高AD=100m,汽车从B点到C点历时14s,则这辆汽车的速度为22.6m/s(精确到0.1)参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236.
如图,小明同学在山顶A处观测到,一辆汽车在一条水平的公路上沿直线匀速行驶,小明在A处测得公路上B,C两点的俯角分别为30°,45°,且∠BAC=135°.若山高AD=100m,汽车从B点到C点历时14s,则这辆汽车的速度为22.6m/s(精确到0.1)参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解甲、乙两个教学班级(每班学生数均为50人)的教学效果,期末考试后,对甲、乙两个班级的学生成绩进行统计分析,画如图甲班学生布线频率分布直方图和乙班学生成绩频数分布表,记成绩不低于80分为优秀.
为了解甲、乙两个教学班级(每班学生数均为50人)的教学效果,期末考试后,对甲、乙两个班级的学生成绩进行统计分析,画如图甲班学生布线频率分布直方图和乙班学生成绩频数分布表,记成绩不低于80分为优秀.| 甲班 | 乙班 | 总计 | |
| 成绩优秀 | 28 | 20 | 48 |
| 成绩不优秀 | 22 | 30 | 52 |
| 总计 | 50 | 50 | 100 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.322 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com