Question

12．为了检测某种产品的质量，抽取了一个容量为100的样本，数据的分组数如下：
[10.75，10.85）3；[10.85，10.95）9；[10.95，11.05）13；[11.05，11.15）16；[11.15，11.25）26；[11.25，11.35）20；[11.35，11.45）7；[11.45，11.55）4；[11.55，11.65）2；    
（1）列出频率分布表含累积频率；
（2）画出频率分布直方图以及频率分布折线图；
（3）据上述图表，估计数据落在[10.95，11.35）范围内的可能性是百分之几？

Answer 1

分析 （1）根据题目中数据进行列表，根据频率=$\frac{频数}{样本容量}$求出每组的频率，画出频率分布表即可；
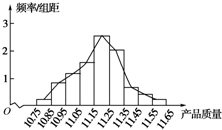
（2）根据用频率除以组距，得到频率分布直方图的纵坐标，然后画出频率分布直方图，最后将矩形的中点连起来得到频率分布折线图；
（3）根据频率分布表中的数据求出落在[10.95，11.35）范围内的频率，从而得到数据落在[10.95，11.35）范围内的可能性；

解答 解：（1）频率分布表如图所示：

分组	频数	频率	累积频率
[10.75，10.85）	3	0.03	0.03
[10.85，10.95）	9	0.09	0.12
[10.95，11.05）	13	0.13	0.25
[11.05，11.15）	16	0.16	0.41
[11.15，11.25）	26	0.26	0.67
[11.25，11.35）	20	0.20	0.87
[11.35，11.45）	7	0.07	0.94
[11.45，11.55）	4	0.04	0.98
[11.55，11.65）	2	0.02	1.00
合计	100	1.00

（2）频率分布直方图及频率分布折线图，如图

（3）由上述图表可知数据落在[10.95，11.35）范围内的频率为1-（0.03+0.09）-（0.07+0.04+0.02）=0.75=75%，
即数据落在[10.95，11.35）范围内的可能性是75%；

点评 本题主要考查了频率分布表，以及概率问题，统计初步在近两年高考中每年都以小题的形式出现，基本上是低起点题．