Question

11．已知在△ABC中，若AB⊥AC、AD⊥BC于D，则$\frac{1}{A{D}^{2}}$=$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$，那么在四面体ABCD中，若AB⊥AC，AB⊥AD，AC⊥AD，AE⊥平面BCD，类比上述结论，你能得到怎样的猜想？写出猜想并给予证明．

Answer 1

分析 利用平面中的射影定理证明；将平面中的三角形类比成空间的三棱锥，三角形的两边垂直类比成三棱锥的三棱垂直，得到类比性质通过作辅助线将空间的证明问题转化为三角形中的性质．

解答 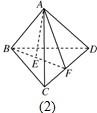解：类比AB⊥AC，AD⊥BC猜想：在四面体ABCD中，若AB⊥AC，AB⊥AD，AC⊥AD，AE⊥平面BCD，则$\frac{1}{A{E}^{2}}$=$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$+$\frac{1}{A{D}^{2}}$．
如图，连接BE交CD于F，连接AF．
∵AB⊥AC，AB⊥AD
∴AB⊥平面ACD．
而AF?平面ACD，∴AB⊥AF．
在Rt△ABF中，AE⊥BF，
∴$\frac{1}{A{E}^{2}}$=$\frac{1}{A{B}^{2}}$+$\frac{1}{A{F}^{2}}$．
在Rt△ACD中，AF⊥CD，
∴$\frac{1}{A{F}^{2}}$=$\frac{1}{A{C}^{2}}$+$\frac{1}{A{D}^{2}}$．
∴$\frac{1}{A{E}^{2}}$=$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$+$\frac{1}{A{D}^{2}}$，故猜想正确

点评 本题考查利用类比推理得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论．