
分析 (I)$\overrightarrow{AC}$=(cosφ+2,sinφ),$\overrightarrow{BC}$=(cosφ,sinφ+2),利用$\overrightarrow{AC}$•$\overrightarrow{BC}$=$\frac{5}{3}$,可得cosφ+sinφ=$\frac{1}{3}$,两边平方即可得出.
(II)由|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{3}$,可得$\sqrt{(cosφ-2)^{2}+si{n}^{2}φ}$=$\sqrt{3}$,化为:cosφ=$\frac{1}{2}$,0<φ<π.解答φ.利用cosθ=$\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}||\overrightarrow{OC}|}$,即可得出.
解答 解:(I)$\overrightarrow{AC}$=(cosφ+2,sinφ),$\overrightarrow{BC}$=(cosφ,sinφ+2),$\overrightarrow{AC}$•$\overrightarrow{BC}$=$\frac{5}{3}$,
∴cosφ(cosφ+2)+sinφ(sinφ+2)=$\frac{5}{3}$,
∴cosφ+sinφ=$\frac{1}{3}$,
两边平方可得:sin2φ=-$\frac{8}{9}$.
(II)∵|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{3}$,∴$\sqrt{(cosφ-2)^{2}+si{n}^{2}φ}$=$\sqrt{3}$,化为:cosφ=$\frac{1}{2}$,∵0<φ<π.
∴φ=$\frac{π}{3}$.
∴C$(\frac{1}{2},\frac{\sqrt{3}}{2})$.
∴cosθ=$\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}||\overrightarrow{OC}|}$=$\frac{-\sqrt{3}}{2×1}$=-$\frac{\sqrt{3}}{2}$,
∴θ=$\frac{5π}{6}$.
即$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为$\frac{5π}{6}$.
点评 本题考查了数量积运算性质、向量夹角公式、三角函数求值,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
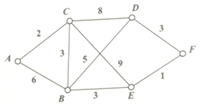 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 女性人数 | 5 | 10 | 15 | 47 | x |
| 男性人数 | 2 | 3 | 10 | y | 2 |
| 女性 | 男性 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(Χ2>k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.
如图,直三棱柱ABC-A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{n(n-1)}$ | B. | $\frac{1}{n(n+1)}$ | C. | $\frac{2}{{{{(n+1)}^2}}}$ | D. | $\frac{3}{(n+1)(n+2)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,2) | C. | (0,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com