
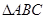 的三边长
的三边长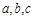 ,满足
,满足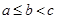
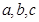 均为正整数,且
均为正整数,且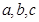 成等差数列,将满足条件的三角形的面积从小到大排成一列
成等差数列,将满足条件的三角形的面积从小到大排成一列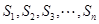 ,且
,且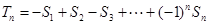 ,求满足不等式
,求满足不等式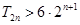 的所有
的所有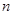 的值;
的值;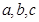 成等比数列,若数列
成等比数列,若数列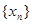 满足
满足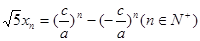 ,证明数列
,证明数列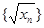 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且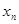 是正整数.
是正整数.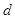 .改成
.改成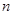 没关系.由于数列
没关系.由于数列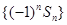 的前
的前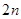 项的和的特点是每项是一项正一项负.所以相邻的两项用平方差公式化简.即可得一个等差数列的求和的式子. 由
项的和的特点是每项是一项正一项负.所以相邻的两项用平方差公式化简.即可得一个等差数列的求和的式子. 由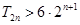 得
得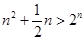 ,由于指数函数是爆炸性的变化,所以要符合该不等式的不是很多,再由
,由于指数函数是爆炸性的变化,所以要符合该不等式的不是很多,再由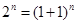 .利用二项式定理展开即可得
.利用二项式定理展开即可得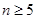 时,
时,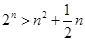 .所以
.所以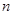 只有2,3,4三种情况.
只有2,3,4三种情况.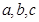 成等比数列.解直角三角形三边的关系可求得
成等比数列.解直角三角形三边的关系可求得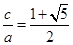 .所以可以写出
.所以可以写出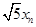 的表达式.在递推一个式子.两式相加,再利用
的表达式.在递推一个式子.两式相加,再利用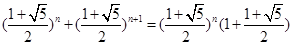 =
=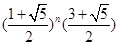 =
=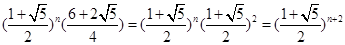 .从而可得
.从而可得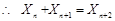 .从而即可得解答结论.再说明前三项符合即可.
.从而即可得解答结论.再说明前三项符合即可.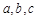 的公差为
的公差为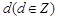 ,则
,则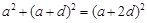
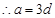
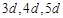 ,面积
,面积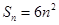 , 2分
, 2分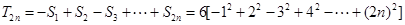
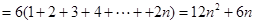
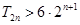 得
得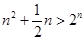 ,
,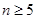 时,
时,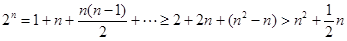 ,
, 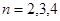 时,
时,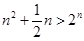 ,当
,当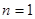 时,
时,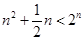
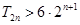 的所有
的所有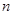 的值为2、3、4 6分
的值为2、3、4 6分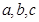 成等比数列,
成等比数列,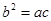 .
.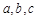 为直角三角形的三边长,知
为直角三角形的三边长,知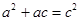 ,
,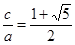 , 8分
, 8分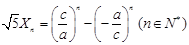 ,得
,得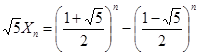 ,
,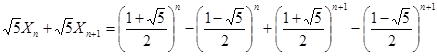
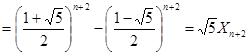
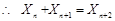 ,则有
,则有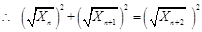 .
.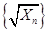 中的任意连续三项为边长均可以构成直角三角形 10分
中的任意连续三项为边长均可以构成直角三角形 10分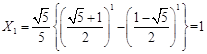 ,
,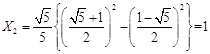
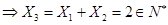 ,由数学归纳法得:
,由数学归纳法得: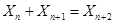 ,同理可得
,同理可得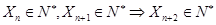 ,
,  都有
都有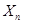 是正整数 12分
是正整数 12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com