练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．你能利用三角函数线求出sin2α+cos2α的值吗？

    分析 如图所示，当角α的终边在坐标轴上时sin2α+cos2α=1．当角α的终边落在四个象限时，利用三角形勾股定理有sin2α+cos2α=1，综合可得结论．

    解答 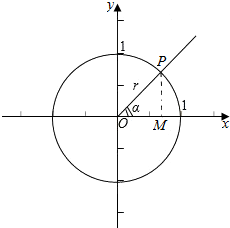证明：当角α的终边在坐标轴上时，正弦线（余弦线）变成一个点，
    而余弦线（正弦线）的长等于r（r=1），
    所以sin2α+cos2α=1．
    当角α的终边落在四个象限时，设角α的终边与单位圆交于点P（x，y）时，过P作PM⊥x轴于点M（如图），
    则|sinα|=|MP|，|cosα|=|OM|，利用三角形勾股定理有sin2α+cos2α=|MP|2+|OM|2=1，
    综上有sin2α+cos2α=1．

    点评 本题主要考查任意角的三角函数的定义，用单位圆中的三角函数线表示三角函数的值，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

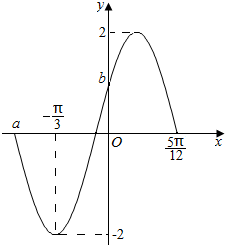    18．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．
    （1）求函数f（x）的解析式；
    （2）求图中a，b的值及函数f（x）的递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知圆C的圆心在射线y=2x-3（x≥0），且与直线y=x+2和y=-x+4都相切．
    （1）求圆C的方程；
    （2）若P（x，y）是圆C上任意一点，求x+2y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知：2•8m•16m=411，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．有一山坡倾斜角为30°，山坡上有一条小路与斜坡底线成45°角，某人沿这条小路向上走了200米，求他实际升高了多少米？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知△ABC的三边长分别为7、9、12，求最长边上的中线长和该三角形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知S，A，B，C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA=AB=2，BC=2$\sqrt{2}$，则球O的表面积等于（　　）
    A．4πB．8πC．12πD．16π

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．设全集U={1，2，3，4}，集合A={1，3}，B={2，3}，则B∩∁UA={2}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知定义域为R的单调减函数f（x）是奇函数，当x＞0时，f（x）=$\frac{x}{3}$-2x．
    （Ⅰ）求f（0）的值；
    （Ⅱ）求f（x）的解析式；
    （Ⅲ）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围．

    查看答案和解析>>

    同步练习册答案