练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知命题P：不等式a2-4a+3＜0的解集；命题Q：使（a-2）x2+2（a-2）x-4＜0对任意实数x恒成立的实数a，若P∨Q是真命题，求实数a的取值范围．

    分析 据复合函数单调性的判定方法，我们可以判断出命题p满足时，参数a的取值范围，进而根据二次不等式恒成立的充要条件，我们易判断出命题q满足时，参数a的取值范围，进而根据p∨q是真命题，易得到满足条件的实数a的取值范围．

    解答 解：不等式a2-4a+3＜0得，1＜a＜3，
    所以命题为； 1＜a＜3，
    由不等式（a-2）x2+2（a-2）x-4＜0对任意实数x恒成立；
    得a
    a=2 或$\left\{\begin{array}{l}a-2＜0\\△=4{（a-2）^2}+16（a-2）＜0\end{array}\right.$，
    解得-2＜a≤2，
    ∵P∨Q是真命题，
    ∴a的取值范围是-2＜a＜3．

    点评 本题考查的知识点是命题的真假判断与应用，函数恒成立问题，其中根据已知求出命题p和q满足时，参数a的取值范围，是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．当双曲线C不是等轴双曲线时，我们把以双曲线C的实轴、虚轴的端点作为顶点的椭圆称为双曲线C的“伴生椭圆”．则离心率为$\sqrt{3}$的双曲线的“伴生椭圆”的离心率为（　　）
    A．$\frac{1}{2}$B．$\frac{{\sqrt{6}}}{3}$C．$\frac{{\sqrt{3}}}{3}$D．$\frac{{\sqrt{2}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知a=0.80.2，b=0.80.5，c=5.20.1，则这三个数的大小关系为（　　）
    A．b＜a＜cB．a＜b＜cC．c＜a＜bD．c＜b＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．如图，从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x 轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率为（　　）
    A．$\frac{1}{2}$B．$\frac{{\sqrt{5}}}{5}$C．$\frac{{\sqrt{2}}}{2}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在△ABC中，若C=90°，三边为a，b，c，则$\frac{a+b}{c}$的范围是（　　）
    A．（$\sqrt{2}$，2）B．（1，$\sqrt{2}$]C．（0，$\sqrt{2}$]D．[$\frac{{\sqrt{2}}}{2}$，$\sqrt{2}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．函数y=f（x）的图象如图所示，则以下描述正确的是（　　）
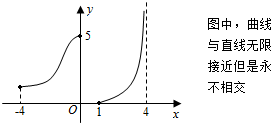
    A．函数f（x）的定义域为[-4，4）
    B．函数f（x）的值域为[0，5]
    C．此函数在定义域内既不是增函数也不是减函数
    D．对于任意的y∈[0，+∞），都有唯一的自变量x与之对应

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设全集U=R，已知集合M={x|x2-x＞0}，N={x|$\frac{x-1}{x}$＜0}，则有（　　）
    A．M∪N=RB．M∩N=∅C．CuN=MD．CvM⊆N

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知cosα=$\frac{3}{5}$，则sin（$\frac{π}{2}$-α）=（　　）
    A．$\frac{3}{5}$B．-$\frac{3}{5}$C．$\frac{4}{5}$D．-$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=4，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$，则$\overrightarrow{a}$•$\overrightarrow{b}$的值是（　　）
    A．2B．±2C．4D．±4

    查看答案和解析>>

    同步练习册答案