Question

13．下列函数中满足$f（\frac{{{x_1}+{x_2}}}{2}）＜\frac{{f（{x_1}）+f（{x_2}）}}{2}（{x_1}≠{x_2}）$的是（　　）

• A． f（x）=3x+2
• B． $f（x）=\sqrt{x}$
• C． $f（x）=-{（\frac{1}{2}）^x}$
• D． f（x）=x²+x+1

Answer 1

分析 可用图表示满足$f（\frac{{x}_{1}+{x}_{2}}{2}）＜\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$的图象，从而由图象看出满足该条件的函数为下凸函数，从而判断每个选项函数的图象是否下凸即可．

解答 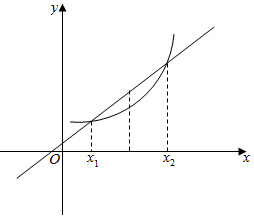解：如图，

可看出满足$f（\frac{{x}_{1}+{x}_{2}}{2}）＜\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$的函数为下凸函数；
根据每个选项函数的图象便可看出只有选项D的二次函数为下凸函数．
故选：D．

点评 考查满足条件$f（\frac{{x}_{1}+{x}_{2}}{2}）＜\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$的函数为下凸函数，并能够用图象加以说明，中点坐标公式，要熟悉一次函数，二次函数，及指数函数，$y=\sqrt{x}$的图象，以及函数关于x轴的对称变换．