
分析 假设f(x)图象上存在两点关于原点对称,设其中一个点横坐标为x,则f(x)+f(-x)=0,x∈(0,π],得出c关于x的函数,求出函数c(x)的值域即c的范围M,则符合条件的c为集合M的补集,得出答案.
解答 解:∵f(x)的图象不过坐标原点,
∴f(0)≠0,即1+c≠0,∴c≠-1.
假设f(x)的图象存在关于坐标原点对称的两点,设两点坐标为(x,f(x)),(-x,-f(x)).x∈(0,π]
则f(x)+f(-x)=0,
∴2x2+2cosx+2c=0,
∴c=-x2-cosx,
∴c′(x)=-2x+sinx<0.
∴c(x)在(0,π]上单调递减,
∴1-π2≤c<-1,
∵f(x)的图象不存在关于坐标原点对称的两点,∴c≥-1或c<1-π2≈-8.87.
又∵c≠-1,
∴c可取到的最大负整数为-9.
故答案为:-9.
点评 本题考查了函数的单调性,函数的值域,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2x+y-8=0 | B. | 3x-2y+1=0 | C. | x+2y-5=0 | D. | 3x+2y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{14}{27}$ | D. | $\frac{14}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
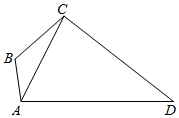 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3x+2 | B. | $f(x)=\sqrt{x}$ | C. | $f(x)=-{(\frac{1}{2})^x}$ | D. | f(x)=x2+x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com