
 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=2BE=4.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=2BE=4.分析 (Ⅰ)根据已知条件便可证明平面BCE∥平面PAD,从而便得到CE∥平面PAD;
(Ⅱ)首先分别以AB,AD,AP三直线为x,y,z轴,建立空间直角坐标系,要使平面DEF⊥平面PCE,便有这两平面的法向量垂直,设F(a,0,0),平面PCE的法向量为$\overrightarrow{m}=(x,y,z)$,根据$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PC}=0}\\{\overrightarrow{m}•\overrightarrow{PE}=0}\end{array}\right.$即可求出$\overrightarrow{m}$,同样的办法表示出平面DEF的法向量$\overrightarrow{n}$,根据$\overrightarrow{m}•\overrightarrow{n}=0$即可求出a,从而求出$\frac{AF}{AB}$.
解答 解:(Ⅰ)证明:BE∥PA,PA?平面PAD,BE?平面PAD;
∴BE∥平面PAD;
同理,∵ABCD为正方形,∴BC∥AD,∴BC∥平面PAD;
又BC∩BE=B;
∴平面EBC∥平面PAD,CE?平面EBC;
∴CE∥平面PAD;
(Ⅱ)分别以边AB,AD,AP所在直线为x,y,z轴,建立如图所示空间直角坐标系,则: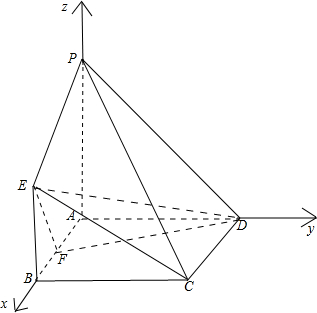
B(4,0,0),C(4,4,0),E(4,0,2),P(0,0,4),D(0,4,0);
∴$\overrightarrow{PC}=(4,4,-4)$,$\overrightarrow{PE}=(4,0,-2)$,$\overrightarrow{PD}=(0,4,-4)$;
设平面PCE的一个法向量为$\overrightarrow m=(x,y,z)$;
∴$\left\{{\begin{array}{l}{\overrightarrow m•\overrightarrow{PC}=0}\\{\overrightarrow m•\overrightarrow{PE}=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{x+y-z=0}\\{2x-z=0}\end{array}}\right.$;
令x=1,则$\left\{{\begin{array}{l}{x=1}\\{y=1}\\{z=2}\end{array}}\right.$,∴$\overrightarrow m=(1,1,2)$;
可设F(a,0,0),则$\overrightarrow{FE}=(4-a,0,2)$,$\overrightarrow{DE}=(4,-4,2)$;
设平面DEF的一个法向量为$\overrightarrow n=(x,y,z)$,则$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{DE}=0}\\{\overrightarrow n•\overrightarrow{FE}=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{2x-2y+z=0}\\{(4-a)x+2z=0}\end{array}}\right.$;
令x=2,则$\left\{{\begin{array}{l}{x=2}\\{y=\frac{a}{2}}\\{z=a-4}\end{array}}\right.$,∴$\overrightarrow n=(2,\frac{a}{2},a-4)$;
由平面DEF⊥平面PCE,得$\overrightarrow m•\overrightarrow n=0$,即$2+\frac{a}{2}+2a-8=0$,$a=\frac{12}{5}<4$;
∴点$F(\frac{12}{5},0,0)$;
∴$\frac{AF}{AB}=\frac{3}{5}$.
点评 考查线面平行、面面平行的判定定理,通过证明直线所在平面和另一平面平行来证明线面平行的方法,通过建立空间直角坐标系,利用空间向量解决面面垂直问题的方法.以及平面法向量的概念及求法,两非零向量垂直的充要条件.


科目:高中数学 来源: 题型:选择题
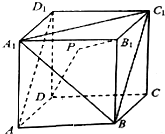 如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )| A. | [0,$\frac{1}{2}$] | B. | [0,$\frac{1}{3}$] | C. | [$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),且经过点($\sqrt{3}$,$\frac{1}{2}$).
如图,在平面直角坐标系xOy中,椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),且经过点($\sqrt{3}$,$\frac{1}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com