
分析 (1)由题意,$\overrightarrow{AB}∥\overrightarrow{BC}$,$\overrightarrow{OA}⊥$$\overrightarrow{OB}$,利用平面向量的坐标表示列出方程组,求出m、n;
(2)由三角形重心的性质,结合平面向量的坐标运算,利用夹角公式即可求出答案.
解答 解:(1)因为三点A,B,C在一条直线上,所以$\overrightarrow{AB}∥\overrightarrow{BC}$,
又$\overrightarrow{AB}=(n+3,2-m)$,$\overrightarrow{BC}=(7-n,1)$,
所以n+3=(7-n)(2-m),①
因为$\overrightarrow{OA}⊥$$\overrightarrow{OB}$,所以-3n+3(m+1)=0,即n=m+1,②
由①、②解得$\left\{\begin{array}{l}m=8\\ n=9\end{array}\right.$,或$\left\{\begin{array}{l}m=1\\ n=2\end{array}\right.$;
(2)因为G为△OAC的重心,且$\overrightarrow{OG}=\frac{2}{3}\overrightarrow{OB}$,
所以点B为线段AC的中点,
所以m=1,n=2;
所以$\overrightarrow{OA}=(-3,2)$,$\overrightarrow{OC}=(7,4)$,
因此$cos∠AOC=\frac{{\overrightarrow{OA}•\overrightarrow{OC}}}{{|\overrightarrow{OA}|•|\overrightarrow{OC}|}}=\frac{-21+8}{{\sqrt{13}•\sqrt{65}}}=-\frac{{\sqrt{5}}}{5}$.
点评 本题考查了平面向量的坐标表示以及三角形重心的性质和平面向量的夹角公式问题,是综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
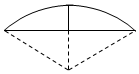 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )| A. | 16平方米 | B. | 18平方米 | C. | 20平方米 | D. | 25平方米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
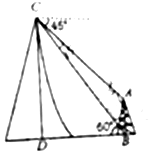 如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.
如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com