考点:用空间向量求平面间的夹角,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)分别以AB,AD,AA1为x轴、y轴、z轴建立空间直角坐标系,由题意,可先假设在棱AA1上存在一点P(0,0,z0),使得DP∥平面B1AE,求出平面B1AE法向量,利用法向量与直线DP的方向向量数量积为0,由此方程解出z0的值,若能解出,则说明存在,若不存在符合条件的t的值,说明不存在这样的点P满足题意.
(2)由题设条件,可求二面角的两个平面的法向量,利用两平面的夹角为30°,建立关于a的方程,解出a的值即可得出AB的长.
解答:
解:(1)分别以AB,AD,AA
1为x轴、y轴、z轴建立空间直角坐标系,
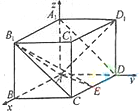
假设在棱AA
1上存在一点P(0,0,z
0)使得DP∥平面B
1AE.此时
=(0,-1,z0)又设AB的长度为a,平面B
1AE的法向量
=(x,y,z),则
=(a,0,1),=(,1,0)∵
⊥平面B
1AE,∴
⊥,⊥,
得
取x=1,使得平面B
1AE的一个法向量
=(1,,-a)…(3分)
要使DP∥平面B
1AE,只要
⊥,有
-az0=0,解得
z0=又DP?平面B
1AE,∴存在点P,满足DP∥平面B
1AE,此时
AP=.…(6分)
(2)连接A
1D,B
1C,由长方体ABCD-A
1B
1C
1D
1及AA
1=AD=1得AD
1⊥A
1D
∵B
1C∥A
1D,∴AD
1⊥B
1C
又由(1)知B
1E⊥AD
1,且B
1C∩B
1E=B
1,
∴AD
1⊥平面DCB
1A
1,
∴
是平面A
1B
1E的一个法向量,此时
=(0,1,1)…(9分)
设
与
所成的角为θ,则
cosθ==∵二面角A-B
1E-A
1的大小为30°
∴|cosθ|=cos30°,即
=,解得a=2,即AB的长为2.…(13分)
点评:本题考查利用空间向量这一工具求二面角,证明线面平行,解题的关键是建立恰当的坐标系及空间位置关系与向量的对应.

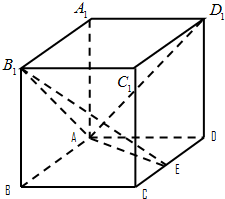 如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.


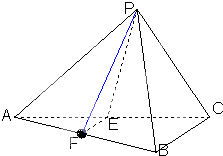 已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB. 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.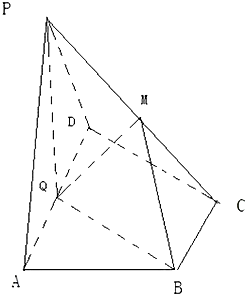 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= 如图,五棱锥P-ABCDE中,PA⊥底面ABCDE,AB∥CD,AC∥ED,AE∥CB,∠ABC=45°,AB=PA=2
如图,五棱锥P-ABCDE中,PA⊥底面ABCDE,AB∥CD,AC∥ED,AE∥CB,∠ABC=45°,AB=PA=2