
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$为非零向量,则“$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为钝角”的充要条件是“$\overrightarrow{a}$•$\overrightarrow{b}$<0” | |
| C. | 若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1>0 | |
| D. | “若θ=$\frac{π}{3}$,则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$,则cosθ$≠\frac{1}{2}$” |
分析 根据特殊情况$\overrightarrow{b}=\overrightarrow{0}$判断A;根据向量数量积的运算和向量夹角的范围判断B;根据特称命题的否定判断C;根据原命题的否命题的定义判断D.
解答 解:A、当$\overrightarrow{b}=\overrightarrow{0}$时,$\overrightarrow{0}$与任何向量都是平行向量,且λ$\overrightarrow{0}$=$\overrightarrow{0}$,A不正确;
B、因为向量夹角的范围是[0°,180°],
所以$\overrightarrow{a}$•$\overrightarrow{b}$<0时,向量的夹角可能是180°,但是$\overrightarrow{a}$,$\overrightarrow{b}$的夹角不是钝角,B不正确;
C、命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1≥0,C不正确;
D、“若θ=$\frac{π}{3}$,则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$,则cosθ$≠\frac{1}{2}$”,D正确,
故选:D.
点评 本题考查命题真假的判断,四种命题的关系,涉及向量的知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [0,4] | B. | (0,4) | C. | (-∞,-4)∪(0,+∞) | D. | (-∞,-4)∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
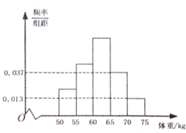 为了了解某校2015年高考准备报考“体育特长生”的学生体重情况,将所得数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前3个小组的频率之比为1:2:3,已知报考“体育特长生”的学生人数是48,则体重在[50,55)组的频数为( )
为了了解某校2015年高考准备报考“体育特长生”的学生体重情况,将所得数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前3个小组的频率之比为1:2:3,已知报考“体育特长生”的学生人数是48,则体重在[50,55)组的频数为( )| A. | 36 | B. | 18 | C. | 12 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 19 | C. | 21 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
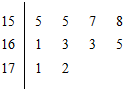 如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.
如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com