
 设椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴长为6,离心率$e=\frac{{\sqrt{6}}}{3}$,O为坐标原点.
设椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴长为6,离心率$e=\frac{{\sqrt{6}}}{3}$,O为坐标原点.分析 (Ⅰ)由a=3,e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,b2=a2-c2=3,即可求得椭圆方程;
(Ⅱ)分类讨论,设直线l1,l2的方程,代入椭圆方程,利用韦达定理及直线的斜率公式分别求得k1、k2、k3、k4,由k1+k2=k3+k4.即可求得直线的l1,l2斜率的乘积m1m2=-$\frac{1}{2}$,根据斜率公式P点坐标,求得出M、N点坐标;
解答 解:(Ⅰ)由2a=6,则a=3,e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,则c=$\sqrt{6}$,b2=a2-c2=3,
∴椭圆标准方程$\frac{x^2}{9}+\frac{y^2}{3}=1$
(Ⅱ)${F_1}({-\sqrt{6},0})$,${F_2}({\sqrt{6},0})$,当直线l1或l2斜率不存在时,P点坐标为$({-\sqrt{6},0})$或$({\sqrt{6},0})$
当直线l1、l2斜率存在时,设斜率分别为m1,m2.
∴l1的方程为$y={m_1}({x+\sqrt{6}})$,l2的方程为$y={m_2}({x-\sqrt{6}})$.
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
联立$\left\{\begin{array}{l}y={m_1}({x+\sqrt{6}})\\ \frac{x^2}{9}+\frac{y^2}{3}=1\end{array}\right.$,得到$({1+3m_1^2}){x^2}+6\sqrt{6}$$m_1^2x+18m_1^2-9=0$,
∴${x_1}+{x_2}=\frac{{-6\sqrt{6}m_1^2}}{1+3m_1^2}$,${x_1}{x_2}=\frac{18m_1^2-9}{1+3m_1^2}$,
同理${x_3}+{x_4}=\frac{{6\sqrt{6}m_2^2}}{1+3m_2^2}$,${x_3}{x_4}=\frac{18m_2^2-9}{1+3m_2^2}$.
∵${k_1}=\frac{y_1}{x_1}=\frac{{{m_1}({{x_1}+\sqrt{6}})}}{x_1}$=${m_1}+\frac{{\sqrt{6}{m_1}}}{x_1}$,${k_2}=\frac{y_2}{x_2}={m_1}+\frac{{\sqrt{6}{m_1}}}{x_2}$,${k_3}=\frac{y_3}{x_3}={m_2}-\frac{{\sqrt{6}{m_2}}}{x_3}$,${k_4}=\frac{y_4}{x_4}={m_2}-\frac{{\sqrt{6}{m_2}}}{x_4}$
又满足k1+k2=k3+k4.$2{m_1}+\frac{{\sqrt{6}{m_1}({{x_1}+{x_2}})}}{{{x_1}{x_2}}}$=$2{m_2}-\frac{{\sqrt{6}{m_2}({{x_3}+{x_4}})}}{{{x_3}{x_4}}}⇒$$2{m_1}+\frac{{\sqrt{6}{m_1}({-6\sqrt{6}m_1^2})}}{18m_1^2-9}$,
=$2{m_2}-\frac{{\sqrt{6}{m_2}•6\sqrt{6}m_2^2}}{18m_2^2-9}$$⇒{m_1}{m_2}=-\frac{1}{2}$,
设点P(x,y),则$\frac{y}{{x+\sqrt{6}}}•\frac{y}{{x-\sqrt{6}}}=-\frac{1}{2}$$⇒\frac{x^2}{6}+\frac{y^2}{3}=1$,($x≠±\sqrt{6}$),
由当直线l1或l2斜率不存在时,P点坐标为$({-\sqrt{6},0})$或$({\sqrt{6},0})$也满足,
∴点P在椭圆$\frac{x^2}{9}+\frac{y^2}{3}=1$上,则存在点M、N其坐标分别为$({-\sqrt{3},0})$、$({\sqrt{3},0})$,使得$|{PM}|+|{PN}|=2\sqrt{6}$为定值.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于难题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2-i}{10}$ | B. | $\frac{1+i}{10}$ | C. | $\frac{4+7i}{10}$ | D. | $\frac{4-i}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在(0,$\frac{π}{4}$)上单调递减 | B. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上单调递减 | ||
| C. | f(x)在(0,$\frac{π}{4}$)上单调递增 | D. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (2,+∞] | C. | (0,2) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BO}=-\frac{5}{6}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$ | B. | $\overrightarrow{BO}=\frac{1}{6}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$ | C. | $\overrightarrow{BO}=\frac{5}{6}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}$ | D. | $\overrightarrow{BO}=-\frac{1}{6}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
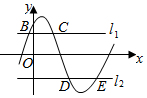 (理)如图,直线l1:y=m(0<m≤A)与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于B、C两点,直线l2:y=-m与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于D、E两点,设B(xB,yB),D(x,yD),记S(m)=|xB-xD|,则S(m)的图象大致是( )
(理)如图,直线l1:y=m(0<m≤A)与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于B、C两点,直线l2:y=-m与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于D、E两点,设B(xB,yB),D(x,yD),记S(m)=|xB-xD|,则S(m)的图象大致是( )| A. | 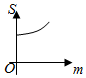 | B. | 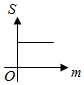 | C. | 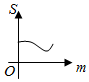 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com