
分析 由|an-an-1|=2n-1,(n∈N,n≥2),可得:|a2n-a2n-1|=22n-1,|a2n+2-a2n+1|=22n+1,根据:数列{a2n-1}是递减数列,且{a2n}是递增数列,可得a2n-a2n-1<a2n+2-a2n+1,可得:a2n-a2n-1=22n-1,同理可得:a2n+1-a2n=-22n,再利用“累加求和”即可得出.
解答 解:由|an-an-1|=2n-1,(n∈N,n≥2),
则|a2n-a2n-1|=22n-1,|a2n+2-a2n+1|=22n+1,
∵数列{a2n-1}是递减数列,且{a2n}是递增数列,
∴a2n-a2n-1<a2n+2-a2n+1,
又∵|a2n-a2n-1|=22n-1<|a2n+2-a2n+1|=22n+1,
∴a2n-a2n-1>0,即a2n-a2n-1=22n-1,
同理可得:a2n+3-a2n+2<a2n+1-a2n,
又|a2n+3-a2n+2|>|a2n+1-a2n|,
则a2n+1-a2n=-22n,
当数列{an}的项数为偶数时,令n=2k(k∈N*),
∴a2-a1=2,a3-a2=-22,a4-a3=23,a5-a4=-24,…,a2015-a2014=-22014,a2016-a2015=22015.
∴a2016-a1=2-22+23-24+…-22014+22015
=$\frac{2[1-(-2)^{2015}]}{1-(-2)}$=$\frac{2}{3}×({2}^{2015}+1)$.
∴a2016=$\frac{{2}^{2016}-1}{3}$.
故答案为:$\frac{{2}^{2016}-1}{3}$.
点评 本题考查了等比数列前n项和公式、数列的单调性,累加法求数列的通项公式,不等式的性质等,同时考查数列的基础知识和化归、分类整合等数学思想,考查了分类讨论方法、推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平移1个位长度,纵坐标不变 | B. | 向右平移1个位长度,纵坐标不变 | ||
| C. | 向左平移$\frac{1}{2}$个位长度,纵坐标不变 | D. | 向右平移$\frac{1}{2}$个位长度,纵坐标不变 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
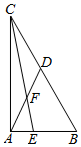 已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}-\overrightarrow{AC}$|=2,D是边BC的中点,$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$
已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}-\overrightarrow{AC}$|=2,D是边BC的中点,$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
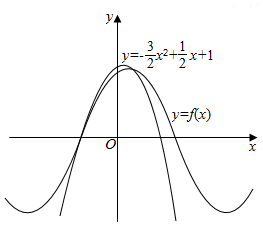 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$).
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com