
 “交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示:
“交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示:| 交通指数 | 频数 | 频率 |
| [0,2) | m1 | n1 |
| [2,4) | m2 | n2 |
| [4,6) | 15 | 0.25 |
| [6,8) | 18 | 0.3 |
| [8,10] | 12 | 0.2 |

| 7 |
| 10 |
| 7 |
| 10 |


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
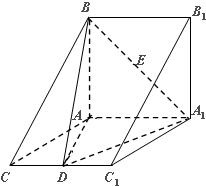 如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.
如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.查看答案和解析>>
科目:高中数学 来源: 题型:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| |||||||
|
. |
| y |
. |
| x |
 |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
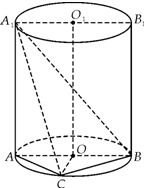 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.查看答案和解析>>
科目:高中数学 来源: 题型:
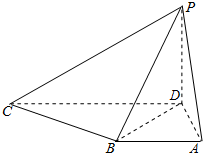 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com