
| A. | 若p:?x∈R,x2-x+1≥0,则¬p:?x∈R,x2-x+1<0 | |
| B. | “$sinθ=\frac{1}{2}$”是“θ=30°或θ=150°”的充分不必要条件 | |
| C. | 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” | |
| D. | 已知p:?x∈R,cosx=1,q:?x∈R,x2-x+2>0,则“p∧(¬q)”为假命题 |
分析 由由特称命题的否定为全称命题,可判断A;
由$sinθ=\frac{1}{2}$,可得θ=k•360°+30°或k•360°+150°,k∈Z,结合充分必要条件的定义,即可判断B;
由命题的否命题形式既对条件否定,又对结论否定,即可判断C;
由cos0=1,判断p真;由配方结合二次函数的性质,判断q真,¬q假,再由复合命题的真值表即可判断D.
解答 解:对于A,若p:?x∈R,x2-x+1≥0,则¬p:?x∈R,x2-x+1<0,由特称命题的否定为全称命题,故A正确;
对于B,$sinθ=\frac{1}{2}$,可得θ=k•360°+30°或k•360°+150°,k∈Z,则“θ=30°或θ=150°”可得“$sinθ=\frac{1}{2}$”,
反之不成立,则为必要不充分条件,故B不正确;
对于C,命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”,由命题的否命题形式既对条件否定,又对结论否定,故C正确;
对于D,p:?x∈R,cosx=1,比如x=0,cos0=1,p真;q:?x∈R,x2-x+2>0,由于x2-x+2=(x-$\frac{1}{2}$)2+$\frac{7}{4}$>0恒成立,q真,¬q假,则“p∧(¬q)”为假命题,故D正确.
故选:B.
点评 本题考查简易逻辑的有关知识,主要是命题的否定、否命题、充分必要条件和复合命题的真假判断,考查判断能力,综合性强,属于基础题.


科目:高中数学 来源: 题型:解答题
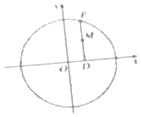 如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.
如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
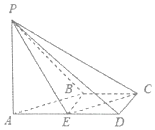 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{5π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
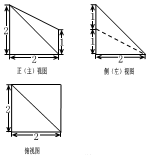
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com