
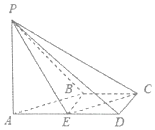
 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.分析 (1)延长AB交直线CD于点M,证明CM∥BE,即可使得直线CM∥平面PBE;
(2)建立如图所示的空间直角坐标系,不妨设AD=2,则$BC=CD=\frac{1}{2}AD=1$.求出平面的法向量,即可求二面角P-CE-B的余弦值.
解答 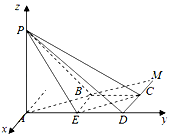 解:(1)延长AB交直线CD于点M,
解:(1)延长AB交直线CD于点M,
∵点E为AD的中点,∴$AE=ED=\frac{1}{2}AD$,
∵$BC=CD=\frac{1}{2}AD$,∴ED=BC,
∵AD∥BC,即ED∥BC.∴四边形BCDE为平行四边形,即EB∥CD.
∵AB∩CD=M,∴M∈CD,∴CM∥BE,
∵BE?平面PBE,CM?PBE∴CM∥平面PBE,…(4分)
∵M∈AB,AB?平面PAB,∴M∈平面PAB,故在平面PAB内可以找到一点M(M=AB∩CD),使得直线CM∥平面PBE…(6分)
(2)如图所示,∵∠ADC=∠PAB=90°,异面直线PA与CD所成的角为90°,即AP⊥CD又AB∩CD=M,
∴AP⊥平面ABCD.
又∠ADC=90°即CD⊥AD
∴CD⊥平面PAD
∴CD⊥PD.
因此∠PDA是二面角P-CD-A的平面角,其大小为45°.
∴PA=AD. …(8分)
建立如图所示的空间直角坐标系,不妨设AD=2,则$BC=CD=\frac{1}{2}AD=1$.
∴P(0,0,2),E(0,1,0),C(-1,2,0),B(-1,1,0)
∴$\overrightarrow{EC}=(-1,1,0)$,$\overrightarrow{PE}$=(0,1,-2),$\overrightarrow{AP}=(0,0,2)$,
易知平面BCE的法向量为${\overrightarrow n_1}=\overrightarrow{AP}=(0,0,2)$
设平面PCE的法向量为${\overrightarrow n_2}=(x,y,z)$,则$\left\{{\begin{array}{l}{\overrightarrow{n_2}•\overrightarrow{PE}=0}\\{\overrightarrow{n_2}•\overrightarrow{EC}=0}\end{array}}\right.$,可得:$\left\{{\begin{array}{l}{y-2z=0}\\{-x+y=0}\end{array}}\right.$.
令y=2,则x=2,z=1,∴${\overrightarrow n_2}=(2,2,1)$. …(10分)
设二面角P-CE-B的平面角为θ,
则$cosθ=|cos<{\overrightarrow n_1},{\overrightarrow n_2}>|$=$\frac{{|\overrightarrow{n_1}•\overrightarrow{n_2}|}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}$=$\frac{2}{{\sqrt{9}×2}}=\frac{1}{3}$.
∴二面角P-CE-B的余弦值为$\frac{1}{3}$. …(12分)
点评 本题考查线面平行,考查线面角,考查向量知识的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p:?x∈R,x2-x+1≥0,则¬p:?x∈R,x2-x+1<0 | |
| B. | “$sinθ=\frac{1}{2}$”是“θ=30°或θ=150°”的充分不必要条件 | |
| C. | 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” | |
| D. | 已知p:?x∈R,cosx=1,q:?x∈R,x2-x+2>0,则“p∧(¬q)”为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{6}$-5 | B. | -5 | C. | 2$\sqrt{6}$+5 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com