
分析 (Ⅰ)求出f(x)的定义域为(0,+∞),求导数,若a≤0,若a>0,判断导函数的符号,然后推出函数的单调性.
(Ⅱ)不妨设x1≤x2,而a<0,由(Ⅰ)知,f(x)在(0,+∞)上单调递增,从而?x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|等价于?x1,x2∈(0,+∞),4x1-f(x1)≥4x2-f(x2),令g(x)=4x-f(x),通过函数的导数求解函数的最值,推出结果.
解答 解:(Ⅰ)f(x)的定义域为(0,+∞),
求导数,得$f'(x)=x+1-a-\frac{a}{x}=\frac{{{x^2}+({1-a})x-a}}{x}=\frac{{({x+1})({x-a})}}{x}$,
若a≤0,则f'(x)>0,此时f(x)在(0,+∞)上单调递增,
若a>0,则由f'(x)=0得x=a,当0<x<a时,f'(x)<0,当x>a时,f'(x)>0,
此时f(x)在(0,a)上单调递减,在(a,+∞)上单调递增.
(Ⅱ)不妨设x1≤x2,而a<0,由(Ⅰ)知,f(x)在(0,+∞)上单调递增,∴f(x1)≤f(x2)
从而?x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|等价于
?x1,x2∈(0,+∞),4x1-f(x1)≥4x2-f(x2)①
令g(x)=4x-f(x),则$g'(x)=4-f'(x)=4-({x+1-a-\frac{a}{x}})=\frac{a}{x}-x+3+a$,
因此,①等价于g(x)在(0,+∞)上单调递减,
∴$g'(x)=\frac{a}{x}-x+3+a≤0$对?x∈(0,+∞)恒成立,
∴$a≤\frac{{{x^2}-3x}}{x+1}$对?x∈(0,+∞)恒成立,∴$a≤{({\frac{{{x^2}-3x}}{x+1}})_{min}}$,
又$\frac{{{x^2}-3x}}{x+1}=x+1+\frac{4}{x+1}-5≥2\sqrt{({x+1})•\frac{4}{x+1}}-5=-1$,
当且仅当$x+1=\frac{4}{x+1}$,即x=1时,等号成立.
∴a≤-1,
故a的取值范围为(-∞,-1].
点评 本题考查函数的导数的应用,考查函数的单调性以及函数的最值的求法,考查分类讨论思想以及转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
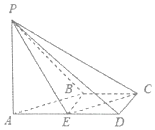 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 294 | B. | 174 | C. | 470 | D. | 304 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{176}{3}$ | B. | $\frac{160}{3}$ | C. | $\frac{128}{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com