
分析 作出图形,求出BO:OD=3:2,设OB=3a,则OD=2a,DE=a,由相交弦定理可得4×2=a×5a,可得a,再利用余弦定理,即可得出结论.
解答  解:如图所示,∵AB=AC=6,AD=4,O是△ABC的外心,
解:如图所示,∵AB=AC=6,AD=4,O是△ABC的外心,
AO平分∠BAC,由内角平分线定理可知:BO:OD=3:2,
设OB=3a,则OD=2a,DE=a,
由相交弦定理可得4×2=a×5a,
∴a=$\sqrt{\frac{8}{5}}$,
∴△ABD中,cosA=$\frac{36+16-40}{2×6×4}$=$\frac{1}{4}$,
△ABC中,BD2=AB2+AD2-2AB•ADcosA=36+9-2×6×3×$\frac{1}{4}$=36,
则BD=6.
故答案为:6.
点评 此题考查了余弦定理,三角形的外心,相交弦定理,熟练掌握余弦定理是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 从12名学生中随机抽泣8人参加活动 | |
| B. | 某单位有210名员工,其中老年员工20人,中年员工40人,青年员工150人,为了解情况,要从中抽取一个容量为21的样本 | |
| C. | 从参加期中考试的1200名高中生随机抽取100人分析作答情况 | |
| D. | 从1200名观众中随机抽取3名幸运观众 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
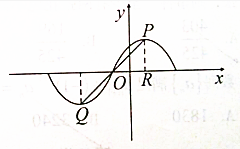 已知函数f(x)=Acos(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$),部分图象如图所示,PQ分别为图象的最高点和最低点,PR⊥x轴于R($\frac{1}{2}$,0)点,∠RPQ=45°,|PQ|=2$\sqrt{2}$.
已知函数f(x)=Acos(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$),部分图象如图所示,PQ分别为图象的最高点和最低点,PR⊥x轴于R($\frac{1}{2}$,0)点,∠RPQ=45°,|PQ|=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -10 | B. | 10 | C. | -$\sqrt{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com