
分析 (1)求出原函数的导函数,得到f′(1),由f′(1)=1求得m值;
(2)求出g(x),求其导函数,可得lnx1=ax1,lnx2=ax2,不等式e1+λ<x1•x2λ恒成立,转化为$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}>\frac{1+λ}{{x}_{1}+λ{x}_{2}}$恒成立,进一步转化为$ln\frac{{x}_{1}}{{x}_{2}}<\frac{(1+λ)({x}_{1}-{x}_{2})}{{x}_{1}+λ{x}_{2}}$恒成立.令$t=\frac{{x}_{1}}{{x}_{2}}$,t∈(0,1),则不等式$lnt<\frac{(1+λ)(t-1)}{t+λ}$在t∈(0,1)上恒成立.令$h(t)=lnt-\frac{(1+λ)(t-1)}{t+λ}$,求导可得满足条件的λ的范围.
解答 解:(1)f′(x)=1+lnx+m,
由题意知,f′(1)=1,即:m+1=1,解得 m=0;
(2)∵e1+λ<x1•x2λ 等价于1+λ<lnx1+λlnx2.
g(x)=f(x)-$\frac{a}{2}$x2-x+a=xlnx-$\frac{a}{2}$x2-x+a,
由题意可知x1,x2 分别是方程g′(x)=0,即:lnx-ax=0的两个根,
即lnx1=ax1,lnx2=ax2.
∴原式等价于1+λ<ax1+λax2=a(x1+λx2),
∵λ>0,0<x1<x2,∴原式等价于$a>\frac{1+λ}{{x}_{1}+λ{x}_{2}}$.
又由lnx1=ax1,lnx2=ax2.
作差得,$ln\frac{{x}_{1}}{{x}_{2}}=a({x}_{1}-{x}_{2})$,即$a=\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$.
∴原式等价于$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}>\frac{1+λ}{{x}_{1}+λ{x}_{2}}$,
∵0<x1<x2,原式恒成立,即$ln\frac{{x}_{1}}{{x}_{2}}<\frac{(1+λ)({x}_{1}-{x}_{2})}{{x}_{1}+λ{x}_{2}}$恒成立.
令$t=\frac{{x}_{1}}{{x}_{2}}$,t∈(0,1),
则不等式$lnt<\frac{(1+λ)(t-1)}{t+λ}$在t∈(0,1)上恒成立.
令$h(t)=lnt-\frac{(1+λ)(t-1)}{t+λ}$,又h′(t)=$\frac{1}{t}-\frac{(1+λ)^{2}}{(t+λ)^{2}}=\frac{(t-1)(t-{λ}^{2})}{t(t+λ)^{2}}$,
当λ2≥1时,可得t∈(0,1)时,h′(t)>0,
∴h(t)在t∈(0,1)上单调增,又h(1)=0,
h(t)<0在t∈(0,1)恒成立,符合题意.
当λ2<1时,可得t∈(0,λ2)时,h′(t)>0,t∈(λ2,1)时,h′(t)<0,
∴h(t)在t∈(0,λ2)时单调增,在t∈(λ2,1)时单调减,又h(1)=0,
∴h(t)在t∈(0,1)上不能恒小于0,不符合题意,舍去.
综上所述,若不等式e1+λ<x1•x2λ 恒成立,只须λ2≥1,
又λ>0,∴λ≥1.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查利用导数求函数的极值,考查数学转化思想方法,训练了学生的灵活变形能力和应用求解能力,属压轴题.


科目:高中数学 来源: 题型:解答题
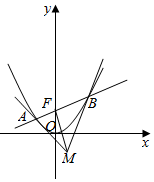 如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.
如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
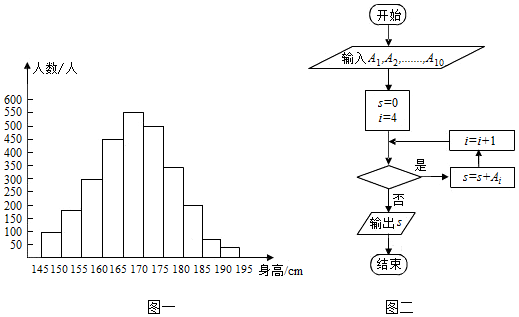
| A. | i<6?,1000 | B. | i<7?,1500 | C. | i<8?,1850 | D. | i<9?,2050 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com