
| A. | $[{\frac{e^2}{8},+∞})$ | B. | $({0,\frac{e^3}{27}}]$ | C. | $[{\frac{e^3}{27},+∞})$ | D. | $({0,\frac{e^2}{8}}]$ |
分析 等式变形为x2${e}^{\frac{y}{x}}$=2ay2成立,构造函数f(t)=$\frac{{e}^{t}}{{t}^{2}}$,求出导函数f'(t)=$\frac{{e}^{t}({t}^{2}-2t)}{{t}^{4}}$,利用导函数求出函数的最值,得出a的范围.
解答 解:${x^2}•{e^{\frac{y}{x}}}-2a{y^2}=0$成立,
∴x2${e}^{\frac{y}{x}}$=2ay2成立,
∴$\frac{{x}^{2}}{{y}^{2}}$${e}^{\frac{y}{x}}$=2a,
令t=$\frac{y}{x}$,
∴2a=$\frac{{e}^{t}}{{t}^{2}}$,
令f(t)=$\frac{{e}^{t}}{{t}^{2}}$,f'(t)=$\frac{{e}^{t}({t}^{2}-2t)}{{t}^{4}}$,
当t>2时,f'(t)>0,f(t)递增,当t<2时,f'(t)<0,f(t)递减,
∴f(t)的最小值为f(2)=$\frac{{e}^{2}}{4}$,
∴2a≥$\frac{{e}^{2}}{4}$,
∴a≥$\frac{{e}^{2}}{8}$
故选A.
点评 本题考查了对问题的转化和导函数的应用.属于基本技巧,应熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 36 | C. | 42 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
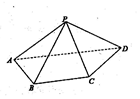 如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.
如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$+$\frac{3}{5}$i | B. | $\frac{4}{5}$-$\frac{3}{5}$i | C. | $\frac{1}{2}$+$\frac{3}{2}$i | D. | $\frac{1}{2}$-$\frac{3}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com