Question

7．用“五点法”作出函数y=1-2sinx，x∈[-π，π]的简图，并回答下列问题：
（1）观察函数图象．写出满足下列条件的x的区间，①y＞1；②y＜1．
（2）若直线y=a与y=1-2sinx，x∈[-π，π]有两个交点，求a的取值范围．

Answer 1

分析 （1）用五点作图法画出函数图象，观察图象，即可写出满足条件的x的区间；
（2）根据图象，用数形结合，判断交点个数．即可求出a的取值范围．

解答 解：用“五点法”作出函数y=1-2sinx，x∈[-π，π]的简图：列表为

x	-π	-$\frac{π}{2}$	0	$\frac{π}{2}$	π
2sinx	0	-2	0	2	0
y=1-sinx	1	3	1	-1	1

画出图形，如图：

（1）观察函数图象．满足①y＞1的x的区间是：（-π，0）
满足②y＜1的x的区间是：（0，π），
（2）若直线y=a与y=1-2sinx，x∈[-π，π]有两个交点，由图象可知：
当1＜a＜3时，直线y=a与y=1-2sinx，x∈[-π，π]有两个交点，
当-1＜a＜1时，直线y=a与y=1-2sinx，x∈[-π，π]有两个交点，
故a的取值范围是：（-1，1）∪（1，3）．

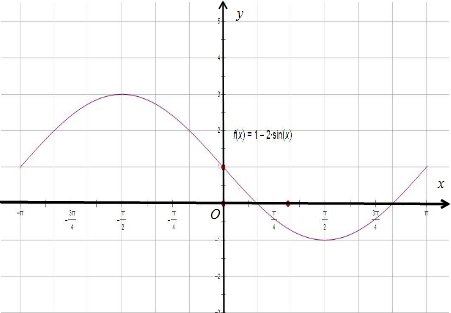
点评 本题考查了正弦函数的图象，考查了五点作图法，数形结合思想是高中重要的一种思想，应熟练灵活掌握，属于基本知识的考查．