
分析 (Ⅰ)根据平行向量的坐标关系即可得到(2-2sinA)(1+sinA)-(sinA+cosA)(sinA-cosA)=0,这样即可解出sin2A,而由A为三角形的内角及$\overrightarrow{AB}•\overrightarrow{AC}$>0,从而判断出A为锐角,这样即可求出A=$\frac{π}{3}$;
(Ⅱ)由B+C=$\frac{2π}{3}$便得C=$\frac{2π}{3}-B$,从而得到$\frac{C-B}{2}=\frac{π}{3}-B$,这样利用二倍角的余弦公式及两角差的正余弦公式即可化简原函数y=1+sin(B-$\frac{π}{6}$),由前面知0$<B<\frac{2π}{3}$,从而可得到B-$\frac{π}{6}$的范围,结合正弦函数的图象即可得到$sin(B-\frac{π}{6})$的范围,这样即可得出原函数的值域.
解答 解:(Ⅰ)由题设知:(2-2sinA)(1+sinA)-(sinA+cosA)(sinA-cosA)=0;
∴2(1-sin2A)-sin2A+cos2A=0;
∴$si{n}^{2}A=\frac{3}{4}$;
又A为三角形内角,所以$sinA=\frac{{\sqrt{3}}}{2}$;
由$\overrightarrow{AB}•\overrightarrow{AC}>0$知A为锐角;
∴$A=\frac{π}{3}$;
(Ⅱ)由(Ⅰ)及题设知:$B+C=\frac{2π}{3}$;
所以:$y=2{sin^2}\frac{B}{2}+cos(\frac{π}{3}-B)=1-cosB+cos(\frac{π}{3}-B)$=$1+\frac{{\sqrt{3}}}{2}sinB-\frac{1}{2}cosB=1+sin(B-\frac{π}{6})$;
又$0<B<\frac{2π}{3}$;
∴$-\frac{π}{6}<B-\frac{π}{6}<\frac{π}{2}$;
∴$-\frac{1}{2}<sin(B-\frac{π}{6})<1$;
∴$y∈(\frac{1}{2}\;,\;2)$;
因此函数$y=2{sin^2}\frac{B}{2}+cos\frac{C-B}{2}$的值域为$(\frac{1}{2}\;,\;2)$.
点评 考查平行向量的坐标的关系,sin2A+cos2A=1,向量数量积的计算公式,已知三角函数值求角,以及三角形的内角和为π,二倍角的余弦公式,两角差的正余弦公式,要熟悉正弦函数的图象.


科目:高中数学 来源: 题型:选择题
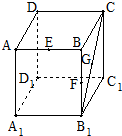 有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{47}{48}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{16}-\frac{{x}^{2}}{12}=1$ | B. | 2x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{18}-\frac{{x}^{2}}{27}=1$ | D. | $\frac{{x}^{2}}{6}-\frac{{y}^{2}}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{24}{25}$ | B. | $\frac{24}{25}$ | C. | $\frac{12}{25}$ | D. | -$\frac{12}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com