
分析 (I).由已知可得:an=2n+a1-2⇒an<an+1<an+2,…,依此类推即可得出;
(II).由(I)可知a1>2,an=2n+a1-2,利用{an}的“伴生三角形”中存在直角三角形及其勾股定理、数列通项公式即可得出.
解答 解:(I).由已知,an=2n+a1-2⇒an<an+1<an+2,
故有an+an+1>an+2⇒an>an+2-an+1=2⇒a1>4-2n(恒成立).
∴a1>2.
(II).由(I)可知a1>2,an=2n+a1-2,
∵{an}的“伴生三角形”中存在直角三角形,∴$a_n^2+a_{n+1}^2=a_{n+2}^2⇒a_n^2=({{a_{n+2}}-{a_{n+1}}})({{a_{n+2}}+{a_{n+1}}})$,
故${(2n+{a_1}-2)^2}=2(4n+2{a_1}+2)$$4{n^2}+(4{a_1}-16)n+{a_1}^2-8{a_1}=0$,化为(2n+a1)(2n+a1-8)=0,
∵a1>2,∴a1=8-2n,∴n=1,2a1=6或a1=4.
∴首项a1的所有可能取值是6或4.
点评 本题考查了新定义“伴生三角形”、勾股定理、数列通项公式、不等式的性质,考查了推理能力与计算能力,属于中档题.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 解:对于集合中最大的数a4,因为a4×a4>a4,3×a4>a4,2×a4>a4. 所以$\frac{a_4}{a_4}$,$\frac{a_4}{3}$,$\frac{a_4}{2}$都属于该集合. 又因为1≤a1<2<3<a4,所以$\frac{a_4}{a_4}<\frac{a_4}{3}<\frac{a_4}{2}<{a_4}$. 所以${a_1}=\frac{a_4}{a_4}=1$,$\frac{a_4}{3}=2,\frac{a_4}{2}=3$,故a1=1,a4=6. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
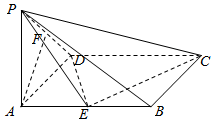 已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com