
【题目】设函数![]() 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求实数k的值;
(2)若![]() ,试判断函数
,试判断函数![]() 的单调性,并求不等式
的单调性,并求不等式![]() 的解集;
的解集;
(3)若![]() ,设
,设![]() ,
,![]() 在
在![]() 上的最小值为-1,求实数m的值.
上的最小值为-1,求实数m的值.
【答案】(1)![]() (2)
(2)![]() 为R上的增函数.
为R上的增函数. ![]() .(3)
.(3)![]()
【解析】
(1)根据函数![]() 是定义域为R的奇函数,得
是定义域为R的奇函数,得![]() ,求得
,求得![]() ,再验证可得值;
,再验证可得值;
(2)由![]() ,解得
,解得![]() 的范围,再根据单调性的定义可证得函数
的范围,再根据单调性的定义可证得函数![]() 的单调性,根据函数的奇偶性可将不等式变形为
的单调性,根据函数的奇偶性可将不等式变形为![]() ,再由函数的单调性可解得不等式的解集;
,再由函数的单调性可解得不等式的解集;
(3)由![]() 可求得
可求得![]() ,从而得出
,从而得出![]() ,再由函数
,再由函数![]() 的值域,讨论二次函数
的值域,讨论二次函数![]() 的对称轴与区间的关系得出最小值,可求得参数的值.
的对称轴与区间的关系得出最小值,可求得参数的值.
(1)因为函数![]() 是定义域为R的奇函数,所以
是定义域为R的奇函数,所以![]() ,即
,即![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() ,符合题意.
,符合题意.
所以![]() .
.
(2)由(1)知![]() ,
,![]() ,解得
,解得![]()
设![]() ,
,![]() 是任意两个实数,且
是任意两个实数,且![]() ,
,
则![]()
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]()
所以![]() ,即
,即![]() ,所以
,所以![]() 为R上的增函数.
为R上的增函数.
因为![]() 是定义域为R的奇函数,所以
是定义域为R的奇函数,所以![]() ,
,
不等式![]() 同解于
同解于![]() .
.
因为![]() 为R上的增函数,所以
为R上的增函数,所以![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
所以不等式![]() 的解集为
的解集为![]() .
.
(3)由![]() 得
得![]() ,解得
,解得![]() .所以
.所以![]() ,
,
![]()
由(2)知![]() 是单调递增函数,因为
是单调递增函数,因为![]() ,所以
,所以![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,
单调递增,![]() 不合题意;
不合题意;
当![]() 时,函数
时,函数![]() 在
在![]() 单调递减,
单调递减,![]() ,解得
,解得![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,![]() ,得
,得![]() (舍去),
(舍去),
综上可得,实数m的值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图为某市国庆节7天假期的楼房认购量与成交量的折线图,小明同学根据折线图对这7天的认购量(单位:套)与成交量(单位:套)作出如下判断:①日成交量的中位数是16;②日成交量超过日平均成交量的有2天;③认购量与日期正相关;④10月7日认购量的增幅大于10月7日成交量的增幅.则上述判断正确的个数为( )
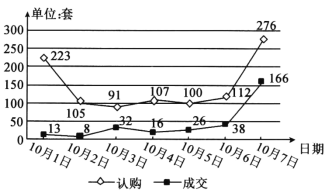
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,焦点到相应准线的距离为
,焦点到相应准线的距离为![]() .
.
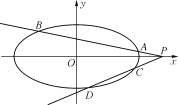
(1) 求椭圆E的标准方程;
(2) 已知P(t,0)为椭圆E外一动点,过点P分别作直线l1和l2,直线l1和l2分别交椭圆E于点A,B和点C,D,且l1和l2的斜率分别为定值k1和k2,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定平面上的五个点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,任意三点不共线.由这些点连成4条线段,每个点至少是一条线段的端点.则不同的连结方式有( ).
,任意三点不共线.由这些点连成4条线段,每个点至少是一条线段的端点.则不同的连结方式有( ).
A. 120种 B. 125种 C. 130种 D. 135种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总 计 | 80 | 320 | 400 |
(1)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式:![]() ,
,

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cos ωx·sin![]() +a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(1)求a和ω的值;
(2)求函数f(x)在[0,π]上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com