
【题目】平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() 的离心率是
的离心率是![]() ,抛物线E:
,抛物线E:![]() 的焦点F是C的一个顶点.
的焦点F是C的一个顶点.
(Ⅰ)求椭圆C的方程;
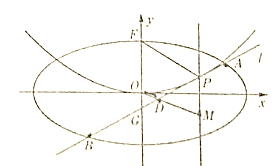
(Ⅱ)设P是E上的动点,且位于第一象限,E在点P处的切线![]() 与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
(i)求证:点M在定直线上;
(ii)直线![]() 与y轴交于点G,记
与y轴交于点G,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标.
【答案】(Ⅰ)![]() ;(Ⅱ)(ⅰ)见解析;(ⅱ)
;(Ⅱ)(ⅰ)见解析;(ⅱ)![]() 的最大值为
的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()
【解析】
试题(Ⅰ)根据椭圆的离心率和焦点求方程;
(Ⅱ)(ⅰ)由点P的坐标和斜率设出直线l的方程和抛物线联立,进而判断点M在定直线上;
(ⅱ)分别列出![]() ,
,![]() 面积的表达式,根据二次函数求最值和此时点P的坐标.
面积的表达式,根据二次函数求最值和此时点P的坐标.
试题解析:(Ⅰ)由题意知:![]() ,解得
,解得![]() .
.
因为抛物线![]() 的焦点为
的焦点为![]() ,所以
,所以![]() ,
,
所以椭圆的方程为![]() .
.
(Ⅱ)(1)设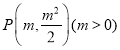 ,由
,由![]() 可得
可得![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() ,其直线方程为
,其直线方程为![]() ,即
,即![]() .
.
设![]() ,联立方程组
,联立方程组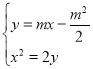
消去![]() 并整理可得
并整理可得![]() ,
,
故由其判别式![]() 可得
可得![]() 且
且![]() ,
,
故![]() ,
,
代入![]() 可得
可得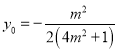 ,
,
因为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
联立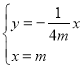 可得点
可得点![]() 的纵坐标为
的纵坐标为![]() ,即点
,即点![]() 在定直线
在定直线![]() 上.
上.
(2)由(1)知直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() ,所以
,所以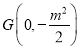 ,
,
又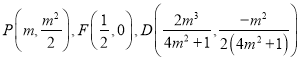 ,
,
所以![]() ,
,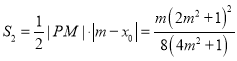 ,
,
所以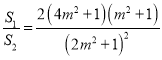 ,令
,令![]() ,则
,则![]() ,
,
因此当![]() ,即
,即![]() 时,
时,![]() 最大,其最大值为
最大,其最大值为![]() ,此时
,此时![]() 满足
满足![]() ,
,
所以点![]() 的坐标为
的坐标为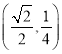 ,因此
,因此![]() 的最大值为
的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为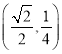 .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() 所示,一条直角走廊宽为
所示,一条直角走廊宽为![]() ,
,![]()


(1)若位于水平地面上的一根铁棒在此直角走廊内,且![]() ,试求铁棒的长
,试求铁棒的长![]() ;
;
(2)若一根铁棒能水平地通过此直角走廊,求此铁棒的最大长度;
(3)现有一辆转动灵活的平板车,其平板面是矩形,它的宽![]() 为
为![]()
![]() 如图2.平板车若想顺利通过直角走廊,其长度
如图2.平板车若想顺利通过直角走廊,其长度![]() 不能超过多少米?
不能超过多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某自来水厂的蓄水池有![]() 吨水,水厂每小时可向蓄水池中注水
吨水,水厂每小时可向蓄水池中注水![]() 吨,同时蓄水池又向居民小区不间断供水,
吨,同时蓄水池又向居民小区不间断供水,![]() 小时内供水总量为
小时内供水总量为![]() 吨,其中
吨,其中![]() .
.
(Ⅰ)从供水开始到第几小时,蓄水池中的存水量最少? 最少水量是多少吨?
(Ⅱ)若蓄水池中水量少于![]() 吨时,就会出现供水紧张现象,请问:在一天的
吨时,就会出现供水紧张现象,请问:在一天的![]() 小时内,大约有几小时出现供水紧张现象?
小时内,大约有几小时出现供水紧张现象?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中以
中以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立坐标系圆
轴非负半轴为极轴建立坐标系圆![]() ,直线
,直线![]() 的极坐标方程分别
的极坐标方程分别
为![]() ,
,![]() .
.
(Ⅰ)求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(Ⅱ)设![]() 为
为![]() 的圆心,
的圆心, ![]() 为
为![]() 与
与![]() 交点连线的中点,已知直线
交点连线的中点,已知直线![]() 的参数方程为
的参数方程为
(![]() 为参数),求
为参数),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,焦距为 2,一条准线方程为
,焦距为 2,一条准线方程为![]() ,
,![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 的坐标为
的坐标为![]() ,求过
,求过![]() 三点的圆的方程;
三点的圆的方程;
(3)若![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如表:
停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为![]() 小时,求
小时,求![]() 的值;
的值;
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠![]() 小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com