
已知a,b∈R,函数f(x)=a+ln(x+1)的图象与g(x)=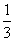 x3-
x3-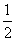 x2+bx的图象在交点(0,0)处有公共切线.
x2+bx的图象在交点(0,0)处有公共切线.
(1)证明:不等式f(x)≤g(x)对一切x∈(-1,+∞)恒成立;
(2)设-1<x1<x2,当x∈(x1,x2)时,证明: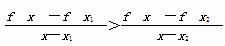 .
.
证明: (1)由题意得f′(x)=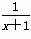 ,g′(x)=x2-x+b,x>-1,
,g′(x)=x2-x+b,x>-1,
则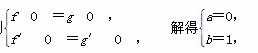
∴f(x)=ln(x+1)(x>-1),g(x)=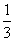 x3-
x3-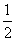 x2+x.
x2+x.
令h(x)=f(x)-g(x)
=ln(x+1)-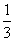 x3+
x3+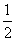 x2-x(x>-1),
x2-x(x>-1),
∴h′(x)=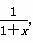 -x2+x-1=-
-x2+x-1=-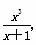 ,
,
∴h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
∴h(x)≤h(0)=0,∴f(x)≤g(x).
(2)当x∈(x1,x2)时,由题意得-1<x1<x<x2,
①设u(x)=(x+1)[f(x)-f(x1)]-(x-x1),
则u′(x)=ln(x+1)-ln(x1+1)>0,
∴u(x)>u(x1)=0,即(x+1)[f(x)-f(x1)]-(x-x1)>0,
∴ >
>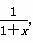 ;
;
②设v(x)=(x+1)[f(x)-f(x2)]-(x-x2),
则v′(x)=ln(x+1)-ln(x2+1)<0,
∴v(x)>v(x2)=0,即(x+1)[f(x)-f(x2)]-(x-x2)>0,
∴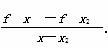 <
<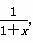 ,
,
由①②得 >
>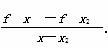 .
.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2,观察发现S′=l;三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V=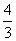 πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.
πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),且.
若直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,则实数k的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com