Question

13£®ÒÑÖªF₁£¬F₂ÊÇÍÖÔ²C£º$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1£¨a£¾b£¾0£©µÄ×ó£¬ÓÒ½¹µã£¬ÀëÐÄÂÊΪ$\frac{1}{2}$£¬M¡¢NÊÇƽÃæÄÚÁ½µã£¬Âú×ã$\overrightarrow{{F}_{1}M}$=-2$\overrightarrow{M{F}_{2}}$£¬Ï߶ÎNF₁µÄÖеãPÔÚÍÖÔ²ÉÏ£¬¡÷F₁MNÖܳ¤Îª12
£¨1£©ÇóÍÖÔ²CµÄ·½³Ì£»
£¨2£©Èô¹ý£¨0£¬2£©µÄÖ±ÏßlÓëÍÖÔ²C½»ÓÚA¡¢B£¬Çó$\overrightarrow{OA}$$•\overrightarrow{OB}$£¨ÆäÖÐOΪ×ø±êÔ­µã£©µÄÈ¡Öµ·¶Î§£®

Answer 1

·ÖÎö £¨1£©ÈçͼËùʾ£¬ÓÉ$\overrightarrow{{F}_{1}M}$=-2$\overrightarrow{M{F}_{2}}$£¬¿ÉµÃµãF₂ÊÇÏ߶ÎF₁NµÄÖе㣮ÓÖÏ߶ÎNF₁µÄÖеãPÔÚÍÖÔ²ÉÏ£¬¿ÉµÃÏ߶ÎPF₂ÊÇ¡÷F₁MNµÄÖÐλÏߣ®ÓÉÍÖÔ²¶¨Òå¼°ÆäÈý½ÇÐÎÖÐλÏ߶ÀÁ¢¼°Æä¡÷F₁MNÖܳ¤Îª12£¬¿ÉµÃ4a+4c=12£¬ÓÖ$\frac{c}{a}$=$\frac{1}{2}$£¬a²=b²+c²£¬ÁªÁ¢½â³ö¼´¿ÉµÃ³ö£®
£¨2£©µ±Ö±Ïßl¡ÍxÖáʱ£¬$\overrightarrow{OA}$$•\overrightarrow{OB}$=-b²=-3£®µ±Ö±ÏßlÓëxÖá²»´¹Ö±Ê±£¬ÉèÖ±ÏßlµÄ·½³ÌΪ£ºy=kx+2£®A£¨x₁£¬y₁£©£¬B£¨x₂£¬y₂£©£®ÓëÍÖÔ²·½³ÌÁªÁ¢»¯Îª£º£¨3+4k²£©x²+16kx+4=0£¬¡÷£¾0£¬»¯Îª£ºk²£¾$\frac{1}{4}$£®ÀûÓÃÒ»Ôª¶þ´Î·½³ÌµÄ¸ùÓëϵÊýµÄ¹Øϵ¼°ÆäÊýÁ¿»ýÔËËãÐÔÖʿɵÃ$\overrightarrow{OA}$$•\overrightarrow{OB}$=-3+$\frac{25}{3+4{k}^{2}}$£¬½ø¶øµÃ³ö½áÂÛ£®

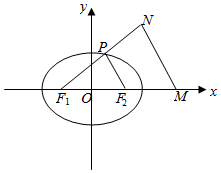½â´ð ½â£º£¨1£©ÈçͼËùʾ£¬¡ß$\overrightarrow{{F}_{1}M}$=-2$\overrightarrow{M{F}_{2}}$£¬¡àµãF₂ÊÇÏ߶ÎF₁NµÄÖе㣬
ÓÖÏ߶ÎNF₁µÄÖеãPÔÚÍÖÔ²ÉÏ£¬¡àÏ߶ÎPF₂ÊÇ¡÷F₁MNµÄÖÐλÏߣ®
¡ß|PF₁|+|PF₂|=2a£¬¡à|NF₁|+|NM|=4a£®
ÓÖ¡÷F₁MNÖܳ¤Îª12£¬¡à4a+4c=12£¬
»¯Îª£ºa+c=3£¬ÓÖ$\frac{c}{a}$=$\frac{1}{2}$£¬a²=b²+c²£¬
½âµÃa=2£¬c=1£¬b²=3£®
¡àÍÖÔ²CµÄ·½³ÌΪ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1£®
£¨2£©µ±Ö±Ïßl¡ÍxÖáʱ£¬$\overrightarrow{OA}$$•\overrightarrow{OB}$=-b²=-3£®
µ±Ö±ÏßlÓëxÖá²»´¹Ö±Ê±£¬ÉèÖ±ÏßlµÄ·½³ÌΪ£ºy=kx+2£®A£¨x₁£¬y₁£©£¬B£¨x₂£¬y₂£©£®
ÁªÁ¢$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$£¬»¯Îª£º£¨3+4k²£©x²+16kx+4=0£¬
¡÷=256k²-16£¨3+4k²£©£¾0£¬»¯Îª£ºk²£¾$\frac{1}{4}$£®
½âµÃ$k£¾\frac{1}{2}$£¬»òk$£¼-\frac{1}{2}$£®
¡àx₁+x₂=-$\frac{16k}{3+4{k}^{2}}$£¬x₁x₂=$\frac{4}{3+4{k}^{2}}$£®
¡à$\overrightarrow{OA}$$•\overrightarrow{OB}$=x₁x₂+y₁y₂=x₁x₂+£¨kx₁+2£©£¨kx₂+2£©
=£¨1+k²£©x₁x₂+2k£¨x₁+x₂£©+4
=£¨1+k²£©¡Á$\frac{4}{3+4{k}^{2}}$-2k¡Á$\frac{16k}{3+4{k}^{2}}$+4
=$\frac{16-12{k}^{2}}{3+4{k}^{2}}$=-3+$\frac{25}{3+4{k}^{2}}$£¬
¡ß$k£¾\frac{1}{2}$£¬»òk$£¼-\frac{1}{2}$£®
¡à$\overrightarrow{OA}$$•\overrightarrow{OB}$¡Ê$£¨-3£¬\frac{13}{4}£©$£®
×ÛÉϿɵãº$\overrightarrow{OA}$$•\overrightarrow{OB}$¡Ê$[-3£¬\frac{13}{4}£©$£®

µãÆÀ ±¾Ì⿼²éÁËÍÖÔ²µÄ¶¨Òå±ê×¼·½³Ì¼°ÆäÐÔÖÊ¡¢Ö±ÏßÓëÍÖÔ²ÏཻÎÊÌâ¡¢Èý½ÇÐÎÖÐλÏ߶¨Àí¡¢Ò»Ôª¶þ´Î·½³ÌµÄ¸ùÓëϵÊýµÄ¹Øϵ¡¢ÏòÁ¿ÊýÁ¿»ýÔËËãÐÔÖÊ¡¢·ÖÀàÌÖÂÛ·½·¨¡¢º¯ÊýÓë²»µÈʽµÄÐÔÖÊ£¬¿¼²éÁËÍÆÀíÄÜÁ¦Óë¼ÆËãÄÜÁ¦£¬ÊôÓÚÄÑÌ⣮