
分析 (1)利用等差数列、三角形的内角和定理可得B,利用正弦定理可得A,进而得到C;
(2)利用等差数列与余弦定理即可得出.
解答 解:(1)由$A+B+C=π,2B=A+C,得B=\frac{π}{3}$.
$由\frac{a}{sinA}=\frac{b}{sinB},得\frac{1}{sinA}=\frac{{\sqrt{3}}}{{\frac{{\sqrt{3}}}{2}}},得sinA=\frac{1}{2}$.
又0<A<B,∴$A=\frac{π}{6}$,∴$C=π-\frac{π}{3}-\frac{π}{6}=\frac{π}{2}$.
∴sinC=1.
(2)证明:由2b=a+c,得4b2=a2+2ac+c2.
∴又b2=a2+c2-ac.
∴4(a2+c2-ac)=a2+2ac+c2.
化为3(a-c)2=0,
∴$a=c.\end{array}$
∴$A=C,又A+C=\frac{2π}{3}$,∴$A=C=B=\frac{π}{3}$.
∴△ABC是等边三角形.
点评 本题考查了等差数列、三角形的内角和定理、正弦定理余弦定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | bf(b)≤af(a) | B. | bf(a)≤af(b) | C. | af(a)≤bf(b) | D. | af(b)≤bf(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | “a、b都是有理数”的否定是“a、b都不是有理数” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | “x=-1”是“x2-5x-6=0”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>e | B. | x1+x2>2 | ||
| C. | x1x2>1 | D. | 有极小值点x0,且x1+x2<2x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥1 | B. | m≥1且m≠1 | C. | m≥1且m≠5 | D. | 0<m<5且m≠1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
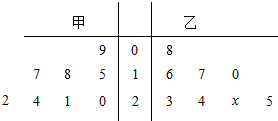 如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.
如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com