Question

7．已知函数f（x）=sinx．若存在x₁，x₂，…，x_m满足0≤x₁＜x₂＜…＜x_m≤6π，且|f（x₁）-f（x₂）|+|f（x₂）-f（x₃）|+…+|f（x_m-1）-f（x_m）|=12（m≥2，m∈N^*），则m的最小值为8．

Answer 1

分析 由正弦函数的有界性可得，对任意x_i，x_j（i，j=1，2，3，…，m），都有|f（x_i）-f（x_j）|≤f（x）_max-f（x）_min=2，要使m取得最小值，尽可能多让x_i（i=1，2，3，…，m）取得最高点，然后作图可得满足条件的最小m值．

解答 解：∵y=sinx对任意x_i，x_j（i，j=1，2，3，…，m），都有|f（x_i）-f（x_j）|≤f（x）_max-f（x）_min=2，
要使m取得最小值，尽可能多让x_i（i=1，2，3，…，m）取得最高点，
考虑0≤x₁＜x₂＜…＜x_m≤6π，|f（x₁）-f（x₂）|+|f（x₂）-f（x₃）|+…+|f（x_m-1）-f（x_m）|=12，
按下图取值即可满足条件，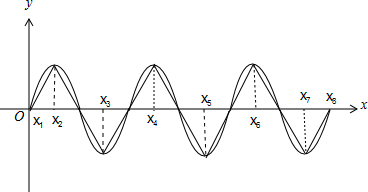

∴m的最小值为8．
故答案为：8．

点评 本题考查正弦函数的图象和性质，考查分析问题和解决问题的能力，考查数学转化思想方法，正确理解对任意x_i，x_j（i，j=1，2，3，…，m），都有|f（x_i）-f（x_j）|≤f（x）_max-f（x）_min=2是解答该题的关键，是难题．