
| x2 |
| 4a2 |
| y2 |
| a2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
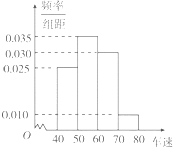 市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速,为调查限速70km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80)分组,绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有
市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速,为调查限速70km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80)分组,绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
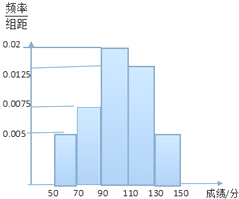 某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.
某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 14 |
| 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
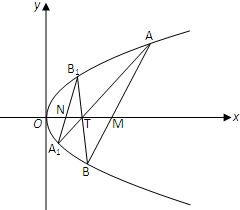 已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.
已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com