
 双流中学食堂旁边有一块矩形空地,学校想要在这块空地上修建一个内接四边形EFGH花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知AB=a(a>10),BC=10,且 AE=AH=CG=CF,设AE=x,花坛EFGH的面积记为S(x).
双流中学食堂旁边有一块矩形空地,学校想要在这块空地上修建一个内接四边形EFGH花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知AB=a(a>10),BC=10,且 AE=AH=CG=CF,设AE=x,花坛EFGH的面积记为S(x).分析 (1)先求得四边形ABCD,△AHE,△BEF的面积,再分割法求得四边形EFGH的面积,即建立y关于x的函数关系式;
(2)由(1)知y是关于x的二次函数,用二次函数求最值的方法求解.
解答 解:(1)S△AEH=S△CFG=$\frac{1}{2}$x2,S△BEF=S△DGH=$\frac{1}{2}$(a-x)(10-x).(2分)
S(x)=SABCD-2S△AEH-2S△BEF=2a-x2-$\frac{1}{2}$(a-x)(10-x)=-2x2+(a+10)x
由$\left\{\begin{array}{l}{x>0}\\{a-x>0}\\{10-x≥0}\\{a>10}\end{array}\right.$,得0<x≤10
∴S(x)=-2x2+(a+10)x,x∈(0,10]…(6分)
(2)由(1)知f(x)=-2x2+(a+10)x=$-2{({x-\frac{a+10}{4}})^2}+\frac{{{{({a+10})}^2}}}{8}$
因为a>10,若$\frac{a+10}{4}$≤10,即10<a≤30,S(x)max=S($\frac{a+10}{4}$)=$(\frac{a+10}{8})^{2}$
$\begin{array}{l}若\frac{a+10}{4}>10,即a>30,有S(x)在上是增函数,此时\\ S{(x)_{max}}=S({10})=-{({10-\frac{a+10}{4}})^2}+\frac{{{{({a+10})}^2}}}{8}=10a-100…(11分)\end{array}$
综上所述,10<a≤30时,S(x)max=S($\frac{a+10}{4}$)=$(\frac{a+10}{8})^{2}$;
当a>30,x=10时,S(x)max=S(10)=10a-100…(12分)
点评 本题主要考查实际问题中的建模和解模能力,考查分类讨论的数学思想,注意二次函数求最值的方法.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=|x| | B. | $y=\root{3}{x^3}$ | C. | $y=\sqrt{x^2}$ | D. | $y=\frac{x^2}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
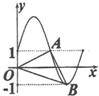
| A. | -10 | B. | -5 | C. | 5 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
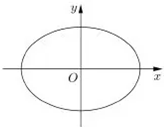 已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,O为坐标原点;
已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,O为坐标原点;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<ω≤$\frac{1}{3}$ | B. | $\frac{1}{4}$<ω≤$\frac{1}{3}$ | C. | 0<ω≤$\frac{1}{4}$ | D. | $\frac{1}{12}$<ω≤$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com