
分析 (1)根据数列的递推公式可得{bn}是首项为1,公差为1的等差数列.
(2)先化简3an-1=3n•2n-1-1,利用利用错位相减求和法求解.
解答 解:(1)证明:由已知得${a_{n+1}}=2{a_n}+{2^n}$,
得${b_{n+1}}=\frac{{{a_{n+1}}}}{2^n}=\frac{{2{a_n}+{2^n}}}{2^n}=\frac{a_n}{{{2^{n-1}}}}+1={b_n}+1$,
∴bn+1-bn=1,
又a1=1,
∴b1=1,
∴{bn}是首项为1,公差为1的等差数列.
(2):由(Ⅰ)知,${b_n}=\frac{a_n}{{{2^{n-1}}}}=n$,
∴${a_n}=n•{2^{n-1}}$,$3{a_n}-1=3n•{2^{n-1}}-1$.
∴${S_n}=3×1×{2^0}+3×2×{2^1}+3×3×{2^2}+…+3(n-1)×{2^{n-2}}+3n×{2^{n-1}}-n$,
两边乘以2,得$2{S_n}=3×1×{2^1}+3×2×{2^2}+…+3(n-1)×{2^{n-1}}+3n×{2^n}-2n$,
两式相减得$-{S_n}=3×(1+{2^1}+{2^2}+…+{2^{n-1}}-n×{2^n})+n$=3×(2n-1-n×2n)-n=3(1-n)2n-3+n,
∴${S_n}=3(n-1)×{2^n}+3-n$.
点评 本题考查数列的通项与求和,解题时要注意错位相减法的合理运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -36 | B. | -9 | C. | 9 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
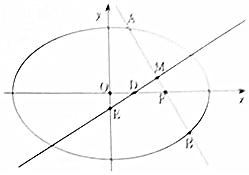 过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.
过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
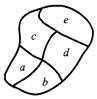 某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )
某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )| A. | 96 | B. | 114 | C. | 168 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 13.2 | m | 14.2 | 15.4 | 16.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
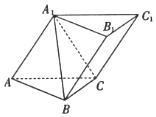 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
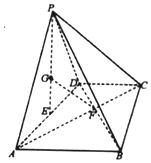 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com