
| A. | $f({{{log}_3}1.2})>f({-\frac{π}{6}})>f({-1})$ | B. | $f({-\frac{π}{6}})>f({{{log}_3}1.2})>f({-1})$ | ||
| C. | $f({-\frac{π}{6}})>f({-1})>f({{{log}_3}1.2})$ | D. | $f({-1})>f({-\frac{π}{6}})>f({{{log}_3}1.2})$ |
分析 求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数值的大小即可.
解答 解:f(x)=x-2sinx,f′(x)=1-2cosx,
令f′(x)>0,解得:2kπ-$\frac{5π}{3}$<x<2kπ-$\frac{π}{3}$,
令f′(x)<0,解得:2kπ-$\frac{π}{3}$<x<2kπ+$\frac{π}{3}$,
故f(x)在(-$\frac{π}{3}$,$\frac{π}{3}$)递减,
而-$\frac{π}{3}$<-1<-$\frac{π}{6}$<3log1.2<$\frac{π}{3}$,
故f(-1)>f(-$\frac{π}{6}$)>f(log31.2),
故选:D.
点评 本题考查了函数的单调性问题,考查导数的应用以及三角函数问题,是一道中档题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | (-∞,0]∪(1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ | B. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{6}$ | C. | x=$\frac{1}{3}$,y=$\frac{1}{6}$,z=$\frac{1}{3}$ | D. | x=$\frac{1}{6}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
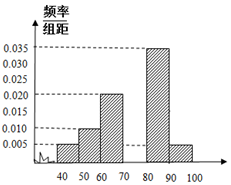 为了估计某校的一次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在[40,100)上,将这些成绩分成六段[40,50),[50,60)…[90,100),后得到如图所示部分频率分布直方图.
为了估计某校的一次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在[40,100)上,将这些成绩分成六段[40,50),[50,60)…[90,100),后得到如图所示部分频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (1,+∞) | C. | (-2,1) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-3,0) | C. | (-2,0) | D. | (-1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com