
分析 根据f(x)有极值,得到f'(x)=0有两个不同的根,求出a、b的关系式,利用几何概型的概率公式即可的得到结论.
解答 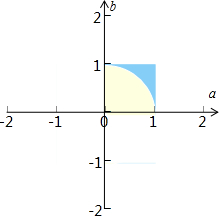 解:在区间[0,1]内随机取两个实数分别为a,b,可得a,b∈[0,1].
解:在区间[0,1]内随机取两个实数分别为a,b,可得a,b∈[0,1].
函数y=$\frac{1}{3}$x3+ax2-(b2-1)x+2有极值,
则f′(x)=x2+2ax-(b2-1)=0有两个不同的根,
即判别式△=4a2+4(b2-1)>0,即a2+b2>1.
如图:
∴由几何概型的概率公式可得对应的概率P=1-$\frac{π}{4}$.
故答案为:1-$\frac{π}{4}$.
点评 本题主要考查几何概型的概率的计算,利用函数取得极值的条件求出对应a的取值范围是解决本题的关键.


科目:高中数学 来源: 题型:解答题
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| 身高x(cm) | 166 | 170 | 172 | 174 | 178 |
| 体重y(kg) | 55 | 60 | 65 | 65 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
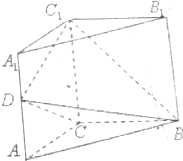 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为( )
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为( )| A. | 90° | B. | 75° | C. | 60° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com