
| A. | f(x)的最小正周期为π | |
| B. | f(x)的图象关于直线x=-$\frac{π}{8}$对称 | |
| C. | f(x)的图象关于点($\frac{π}{8}$,0)对称 | |
| D. | f(x)的图象向右平移$\frac{π}{8}$后得到一个偶函数的图象 |
分析 利用三角函数中的恒等变换应用化简函数解析式可得f(x)=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)+$\frac{1}{2}$,利用正弦函数的图象和性质即可逐一判断得解.
解答 解:∵f(x)=sinx(cosx+sinx)=$\frac{1}{2}$sin2x+$\frac{1-cos2x}{2}$=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)+$\frac{1}{2}$,
∴f(x)的最小正周期T=$\frac{2π}{2}=π$,故A正确;
由sin[2×(-$\frac{π}{8}$)-$\frac{π}{4}$]=-1,故B正确;
由f($\frac{π}{8}$)=$\frac{\sqrt{2}}{2}$sin(2×$\frac{π}{8}$-$\frac{π}{4}$)+$\frac{1}{2}$=$\frac{1}{2}$,故C错误;
将f(x)的图象向右平移$\frac{π}{8}$后得到y=$\frac{\sqrt{2}}{2}$sin[2(x-$\frac{π}{8}$)-$\frac{π}{4}$]+$\frac{1}{2}$=$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$cos2x为偶函数,故D正确.
故选:C.
点评 本题逐一考查了三角函数中的恒等变换应用,考查了正弦函数的图象和性质,周期公式的应用,考查了数形结合思想,属于中档题.


科目:高中数学 来源: 题型:选择题
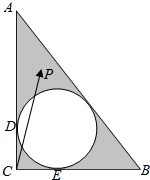 在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )
在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [1200,1800) | x | A |
| [1800,2400) | 90 | B |
| [2400,3000) | y | 0.40 |
| [3000,3600) | 160 | 0.32 |
| [3600,4200] | z | 0.04 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-2y-6=0 | B. | 2x-3y+6=0 | C. | 3x+2y-6=0 | D. | 2x+3y+6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{{e}_{1}}$=(-2,3),$\overrightarrow{{e}_{2}}$=(4,-6) | B. | $\overrightarrow{{e}_{1}}$=(1,5),$\overrightarrow{{e}_{2}}$=(-2,1) | ||
| C. | $\overrightarrow{{e}_{1}}$=(2,3),$\overrightarrow{{e}_{2}}$=(-1,-$\frac{3}{2}$) | D. | $\overrightarrow{{e}_{1}}$=(3,4),$\overrightarrow{{e}_{2}}$=(-6,-8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com