Question

4．函数f（x）=$\left\{\begin{array}{l}ln（-x）+a，x＜0\\ f（x+1），x≥0\end{array}$，a∈R，当0≤x＜1时，f（x）=1-x，则f（x）的零点个数为（　　）

• A． O
• B． 1
• C． 2
• D． 无穷多个

Answer 1

分析 讨论x＜0时，函数的零点；再由x≥0时，f（x）为最小正周期为1的函数，且0≤x＜1时，f（x）=1-x，画出f（x）的大致图象，通过图象观察，即可得到f（x）的零点个数．

解答 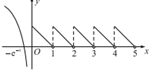解：函数f（x）=$\left\{\begin{array}{l}ln（-x）+a，x＜0\\ f（x+1），x≥0\end{array}$，a∈R，
当x＜0时，必存在x=-e^-a＜0，使得f（x₀）=0，
即?a∈R，f（x）在（-∞，0）内必有一个零点；
当x≥0时，f（x）为最小正周期为1的函数，
且0≤x＜1时，f（x）=1-x，
画出f（x）的大致图象，
可得函数的零点个数为1．
故选：B．

点评 本题考查函数的零点个数问题的解法，注意运用函数的性质：周期性，考查数形结合的思想方法，属于中档题．