
分析 (Ⅰ)通过联立a1+a5=10、S4=16可知首项和公差,进而可知an=2n-1;通过作差可知当n≥2时bn=$\frac{1}{{3}^{n}}$,进而可得结论;
(Ⅱ)通过(I)anbn=(2n-1)$\frac{1}{{3}^{n}}$,进而利用错位相减法计算即得结论.
解答 解:(Ⅰ)依题意,$\left\{\begin{array}{l}{2{a}_{1}+4d=10}\\{4{a}_{1}+6d=16}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=2}\end{array}\right.$,
∴an=1+2(n-1)=2n-1;
∵b1+3b2+32b3+…+3n-1bn=$\frac{n}{3}$,
∴b1+3b2+32b3+…+3n-2bn-1=$\frac{n-1}{3}$(n≥2),
两式相减得:3n-1bn=$\frac{n}{3}$-$\frac{n-1}{3}$=$\frac{1}{3}$,
∴bn=$\frac{1}{{3}^{n}}$(n≥2),
又∵b1=$\frac{1}{3}$满足上式,
∴数列{bn}的通项公式bn=$\frac{1}{{3}^{n}}$;
(Ⅱ)由(I)可知anbn=(2n-1)$\frac{1}{{3}^{n}}$,
则Tn=1•$\frac{1}{3}$+3•$\frac{1}{{3}^{2}}$+…+(2n-1)$\frac{1}{{3}^{n}}$,
$\frac{1}{3}$Tn=1•$\frac{1}{{3}^{2}}$+3•$\frac{1}{{3}^{3}}$+…+(2n-3)$\frac{1}{{3}^{n}}$+(2n-1)$\frac{1}{{3}^{n+1}}$,
两式相减得:$\frac{2}{3}$Tn=$\frac{1}{3}$+2($\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$)-(2n-1)$\frac{1}{{3}^{n+1}}$
=2•$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$-$\frac{1}{3}$-(2n-1)$\frac{1}{{3}^{n+1}}$
=$\frac{2}{3}$[1-(n+1)$\frac{1}{{3}^{n}}$],
∴Tn=1-(n+1)$\frac{1}{{3}^{n}}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
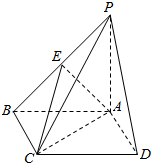 在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,E为PB的中点.
在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,E为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
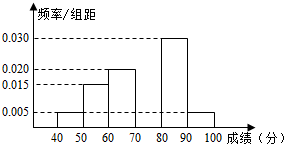 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 0 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (1,0) | C. | (2,0) | D. | (4,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
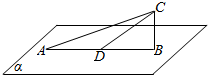 如图,平面α⊥平面ABC,D为线段AB的中点,|AB|=2$\sqrt{3}$,∠CDB=30°,P为面α内的动点,且P到直线CD的距离为1,则∠APB的最大值为 )
如图,平面α⊥平面ABC,D为线段AB的中点,|AB|=2$\sqrt{3}$,∠CDB=30°,P为面α内的动点,且P到直线CD的距离为1,则∠APB的最大值为 )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com