
分析 (Ⅰ)先求出函数的定义域,再根据偶函数的定义即可证明,
(Ⅱ)代入求值即可.
解答 证明:(Ⅰ)$\left\{\begin{array}{l}{2+x>0}\\{2-x>0}\end{array}\right.$ 解得-2<x<2
∴f(x)的定义域为(-2,2)
又当x∈(-2,2)时,有-x∈(-2,2),
f(-x)=log2(2-x)+log2(2+x)=f(x).
∴f(x)为偶函数.
(Ⅱ)f(x)=log2(2+x)+log2(2-x)=log2(4-x2),
∴f($\sqrt{3}$)=log2(4-3)=0.
点评 本题考查了偶函数的定义以及对数函数的运算性质,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 简单随机抽样、系统抽样、分层抽样 | B. | 简单随机抽样、分层抽样、系统抽样 | ||
| C. | 系统抽样、分层抽样、简单随机抽样 | D. | 系统抽样、简单随机抽样、分层抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
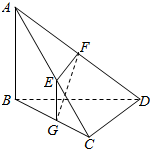 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com