
| A. | (-1,0) | B. | (1,0) | C. | (2,0) | D. | (4,0) |
分析 求出切线方程,确定M,N的坐标,验证$\overrightarrow{MF}$•$\overrightarrow{NF}$=0,即可得出结论.
解答 解:设M($\frac{{{y}_{0}}^{2}}{4}$,y0)(y0>0),y=2$\sqrt{x}$,则y′=$\frac{1}{\sqrt{x}}$,
∴直线l的方程为y-y0=$\frac{2}{{y}_{0}}$(x-$\frac{{{y}_{0}}^{2}}{4}$),
设x=-1,则y=-$\frac{2}{{y}_{0}}$+$\frac{{y}_{0}}{2}$,
∴$\overrightarrow{MF}$•$\overrightarrow{NF}$=(1-$\frac{{{y}_{0}}^{2}}{4}$,-y0)•(2,$\frac{2}{{y}_{0}}$-$\frac{{y}_{0}}{2}$)=2-$\frac{{{y}_{0}}^{2}}{2}$-2+$\frac{{{y}_{0}}^{2}}{2}$=0,
∴MF⊥NF,
∴以MN为直径的圆过x轴上一个定点P(1,0),
故选:B.
点评 本题考查抛物线的方程与性质,考查向量知识的运用,属于中档题.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 简单随机抽样、系统抽样、分层抽样 | B. | 简单随机抽样、分层抽样、系统抽样 | ||
| C. | 系统抽样、分层抽样、简单随机抽样 | D. | 系统抽样、简单随机抽样、分层抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在x∈Z,使2x+m>0 | B. | 不存在x∈Z,使2x+m>0 | ||
| C. | 对任意x∈Z,都有2x+m≤0 | D. | 对任意x∈Z,都有2x+m>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
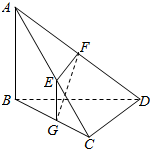 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com