
 如图,在正三棱柱ABC-A1B1C1中,D为AB的中点,AA1=4,AB=6,则异面直线B1D与AC1所成角的余弦值为$\frac{5\sqrt{13}}{26}$.
如图,在正三棱柱ABC-A1B1C1中,D为AB的中点,AA1=4,AB=6,则异面直线B1D与AC1所成角的余弦值为$\frac{5\sqrt{13}}{26}$. 分析 直接找异面直线所成的角不好找,所以可以考虑用向量解决,去求向量$\overrightarrow{{B}_{1}D}$和向量$\overrightarrow{A{C}_{1}}$的夹角,通过图形知道$\overrightarrow{A{C}_{1}}=\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}D}=-\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{BA}$,所以根据已知的边角的大小及数量积的运算求$\sqrt{(\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{C}_{1}})^{2}}$,$\sqrt{(-\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{BA})^{2}}$,$(\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{C}_{1}})•(-\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{BA})$,这样根据向量夹角的余弦公式即可求出向量$\overrightarrow{{B}_{1}D}$和向量$\overrightarrow{A{C}_{1}}$夹角的余弦,根据异面直线所成角的范围,从而得出要求的异面直线夹角的余弦值.
解答 解:如图, $\overrightarrow{{AC}_{1}}=\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}D}=-\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{BA}$;
$\overrightarrow{{AC}_{1}}=\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}D}=-\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{BA}$;
∴$\overrightarrow{A{C}_{1}}•\overrightarrow{{B}_{1}D}$=$-{\overrightarrow{A{A}_{1}}}^{2}+\frac{1}{2}\overrightarrow{A{A}_{1}}•\overrightarrow{BA}$$-\overrightarrow{{A}_{1}{C}_{1}}•\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{{A}_{1}{C}_{1}}•\overrightarrow{BA}$=-16+0-0-9=-25;
$|\overrightarrow{A{C}_{1}}|=\sqrt{(\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{C}_{1}})^{2}}=\sqrt{16+0+36}=2\sqrt{13}$,$|\overrightarrow{{B}_{1}D}|=\sqrt{(-\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{BA})^{2}}$=$\sqrt{16+0+9}=5$;
$cos<\overrightarrow{A{C}_{1}},\overrightarrow{{B}_{1}D}>=\frac{-25}{2\sqrt{13}•5}$=$-\frac{5\sqrt{13}}{26}$;
∴异面直线B1D和AC1所成角的余弦值为$\frac{5\sqrt{13}}{26}$.
故答案为:$\frac{5\sqrt{13}}{26}$.
点评 考查向量加法的几何意义,共线向量,两非零向量垂直的充要条件,以及向量数量积的运算,利用|$\overrightarrow{a}$|=$\sqrt{{\overrightarrow{a}}^{2}}$求向量$\overrightarrow{a}$的长度,向量夹角余弦的计算公式,异面直线所成角的范围.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.
如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
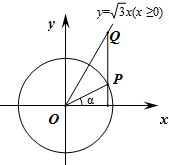 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com