
分析 (1)根据对一切实数x,y∈R都有f(x+y)-f(y)=x(x+2y+1)成立,且题中已经给出了f(1)=0,要求的值是f(0),所以,令x=1,y=0即可求f(0);
(2)在(1)中已经求出了f(0)的值,只需在给出的等式中取y=0即可求 f(x)的解析式,(0,4)上存在实数x0,使得f(x0)+6=ax0成立,分离参数,求出参数的取值范围即可.
解答 解:(1)因为函数f(x)对一切实数x,y都有f(x+y)-f(y)=x(x+2y+1)成立.且f(1),所以令x=1,y=0,
代入上式得f(1)-f(0)=2,
所以f(0)=-2.
(2)因为函数f(x)对一切实数x,y都有f(x+y)-f(y)=x(x+2y+1)成立,所以令y=0,代入上式得
f(x)-f(0)=x(x+1),又由(1)知f(0)=-2,
所以f(x)=x(x+1)-2,
因为f(x0)+6=ax0成立,
即x0(x0+1)-2+6=ax0在(0,4)上成立,
所以a=x0+1+$\frac{4}{{x}_{0}}$≥2$\sqrt{{x}_{0}\frac{4}{{x}_{0}}}$+1=5,当且仅当x0=2时取等号,
所以a≥5.
点评 本题考查抽象函数及其应用,解决抽象函数的问题一般应用赋值法.关键是结合已知条件和要求的结论对变量恰当赋值.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
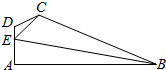 如图所示,在平面四边形ABCD中,AB⊥AD,∠ADC=$\frac{2π}{3}$,E为AD边上一点,CE=$\sqrt{7}$,DE=1,AE=2,∠BEC=$\frac{π}{3}$.
如图所示,在平面四边形ABCD中,AB⊥AD,∠ADC=$\frac{2π}{3}$,E为AD边上一点,CE=$\sqrt{7}$,DE=1,AE=2,∠BEC=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com