
| x | $\sqrt{2}$ | 2 | 4 |
| y | $\frac{\sqrt{2}}{2}$ | 0 | 4 |
分析 (1)利用抛物线与椭圆的简单性质判断点的坐标所在曲线,然后求解抛物线方程椭圆方程.
(2)设M(x1,y1),N(x2,y2).把直线方程与椭圆的方程联立得到关于y的一元二次方程,利用根与系数的关系能求出m的值.
解答 解:(1)因为椭圆与抛物线的中心在原点,焦点坐标在x轴上,所以(2,0)是椭圆上的点,(4,4)是抛物线上的点,($\sqrt{2},\frac{\sqrt{2}}{2}$)是椭圆上的点,
设抛物线C2的方程为:y2=2px,可得16=8p,解得p=2,抛物线C2的方程为:y2=4x,
设椭圆方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{{b}^{2}}=1$,可得$\frac{{(\sqrt{2})}^{2}}{4}+\frac{{(\frac{\sqrt{2}}{2})}^{2}}{{b}^{2}}=1$,解得b2=1.
椭圆C1的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)设M(x1,y1),N(x2,y2).
联立$\left\{\begin{array}{l}x=my+1\\ \frac{{x}^{2}}{4}+{y}^{2}=1\end{array}\right.$,得(m2+4)y2+2my-3=0,
∴y1+y2=-$\frac{2m}{{m}^{2}+4}$,y1y2=-$\frac{3}{{m}^{2}+4}$.
∴x1x2=m2y1y2+m(y1+y2)+1
=$\frac{-3{m}^{2}}{{m}^{2}+4}$+$\frac{-2{m}^{2}}{{m}^{2}+4}$+1
=$\frac{4-4{m}^{2}}{{m}^{2}+4}$.
∵$\overrightarrow{OM}⊥\overrightarrow{ON}$,∴x1x2+y1y2=0,
∴$\frac{4-4{m}^{2}}{{m}^{2}+4}$=0
解得m=±1.
点评 本题综合考查了:椭圆与抛物线的标准方程及其性质,把直线方程与椭圆的方程联立得到关于y的一元二次方程得到根与系数的关系,直线的垂直与向量的数量积的关系的应用.需要较强的推理能力和计算能力.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
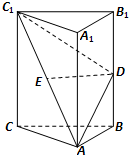 如图,在直三棱柱ABC-A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
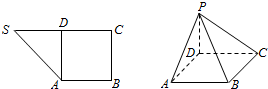 如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com