Question

18．己知x，y为实数，代数式$\sqrt{1+（y-2）^{2}}$+$\sqrt{9+（3-x）^{2}}$+$\sqrt{{x}^{2}+{y}^{2}}$的最小值是$\sqrt{5}$+3$\sqrt{2}$．

Answer 1

分析 根据$\sqrt{1+（y-2）^{2}}$+$\sqrt{9+（3-x）^{2}}$+$\sqrt{{x}^{2}+{y}^{2}}$的几何意义结合图象求出最小值即可．

解答 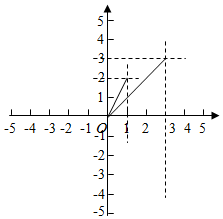解：$\sqrt{1+（y-2）^{2}}$的几何意义表示（0，y），（1，2）的距离，
$\sqrt{9+（3-x）^{2}}$的几何意义表示（x，0），（3，3）的距离，
$\sqrt{{x}^{2}+{y}^{2}}$的几何意义表示（x，y），（0，0）的距离，
如图示：
，
结合图象x=0，y=0时，
代数式$\sqrt{1+（y-2）^{2}}$+$\sqrt{9+（3-x）^{2}}$+$\sqrt{{x}^{2}+{y}^{2}}$的最小值是$\sqrt{5}$+3$\sqrt{2}$，
故答案为：$\sqrt{5}$+3$\sqrt{2}$．

点评 本题考查了求函数的最值问题，考查数形结合思想，是一道中档题．