
| 1 |
| xn+1 |
| 1 |
| xn |
| n-1 |
| n |
| 1 |
| xn |
xn×
|
| 1 |
| xn |
| 1 |
| xn |
| 1 |
| xn+1 |
| 1 |
| xn |
| 1 |
| xn+1 |
| k-1 |
| k |
| 1 |
| xn+1 |
| 1 |
| 2-xk |
| 1 | ||
2-
|
| k |
| k+1 |
| n-1 |
| n |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、2
| ||
B、
| ||
| C、3 | ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB折痕为AB′,AB′交DC于点P,当凹多边形ACB′PD的面积最大时制冷效果最好.
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB折痕为AB′,AB′交DC于点P,当凹多边形ACB′PD的面积最大时制冷效果最好.查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-a |
| ax |
查看答案和解析>>
科目:高中数学 来源: 题型:
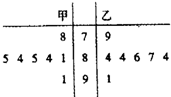 为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.
为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com