练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    判断下列函数的奇偶性．f(x)＝.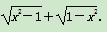


    f(x)的定义域为{－1,1}，关于原点对称．

    又f(－1)＝f(1)＝0，f(－1)＝－f(1)＝0，

    所以f(x)既是奇函数又是偶函数．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知命题p：若x∈N*，则x∈Z.命题q：∃x0∈R，x0－1＝0.则下列命题为真命题的是(　　)

    A．綈p                                  B．p∧q

    C．綈p∨q                               D．綈p∨綈q

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝的值域为[－2,2]，则实数a的取值范围是(　　)

    A．[0，＋∞) B．[0,3]

    C．[－3,0] D．(－3,0)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)在实数集R上具有下列性质：①直线x＝1是函数f(x)的一条对称轴；②f(x＋2)＝－f(x)；③当1≤x1<x2≤3时，[f(x2)－f(x1)](x2－x1)<0，则f(2 011)，f(2 012)，f(2 013)从大到小的顺序为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是奇函数，且在(0，＋∞)内是增函数，又f(－3)＝0，则x·f(x)<0的解集是(　　)

    A．{x|－3<x<0，或x>3}

    B．{x|x<－3，或0<x<3}

    C．{x|x<－3，或x>3}

    D．{x|－3<x<0，或0<x<3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)，g(x)分别是定义在R上的奇函数和偶函数，且f(x)－g(x)＝x，则f(1)，g(0)，g(－1)之间的大小关系是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设二次函数f(x)＝ax2－2ax＋c在区间[0,1]上单调递减，且f(m)≤f(0)，则实数m的取值范围是(　　)

    A．(－∞，0]                            B．[2，＋∞)

    C．(－∞，0]∪[2，＋∞)                 D．[0,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝a|2x－4|(a>0，a≠1)满足f(1)＝，则f(x)的单调递减区间是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝则函数y＝f(x)－(x2＋1)的零点个数为(　　)

    A．1                                    B．2

    C．3                                    D．4

    查看答案和解析>>

    同步练习册答案