
分析 利用圆锥的底面半径和高相等,侧面积为4$\sqrt{2}$π,求出圆锥的底面半径,再利用等体积法求出圆锥底面中心到截面的距离.
解答 解:设圆锥的底面半径为r,则高r,母线长为$\sqrt{2}$r,
∵侧面积为4$\sqrt{2}$π,
∴$πr•\sqrt{2}r$=4$\sqrt{2}$π,
∴r=2,
∵过圆锥的两条母线作截面,截面为等边三角形,
∴S截面=$\frac{\sqrt{3}}{4}•(2\sqrt{2})^{2}$=2$\sqrt{3}$,
设圆锥底面中心到截面的距离为h,则由等体积可得$\frac{1}{3}•2\sqrt{3}h$=$\frac{1}{3}•\frac{1}{2}•2•2•2$,
∴h=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查圆锥的侧面积,考查体积的计算,考查学生的计算能力,正确运用等体积法是解题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
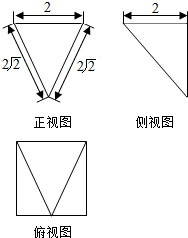
| A. | $\frac{4\sqrt{6}}{3}$ | B. | 2$\sqrt{6}$ | C. | $\frac{4\sqrt{7}}{3}$ | D. | 4$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.
如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
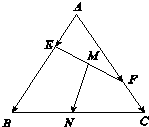 如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在以棱长为1的正方形ABCD-A1B1C1D1中,求:
在以棱长为1的正方形ABCD-A1B1C1D1中,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份 | 第一季度 | 第二季度 | 第三季度 | 第四季度 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 产量 | 500 | 400 | 625 | 625 | 500 | 500 | 500 | 500 | 500 | 400 | 400 | 625 |
| 零件市场价格 | 8 | 10 |
| 概率 | 0.4 | 0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.
如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com