
分析 (1)设椭圆方程,由a=$\sqrt{2}$b,a2=b2+1,即可求得a和b的值,求得椭圆方程的标准方程;
(2)由向量数量积的坐标运算求得$\overrightarrow{PA}$?$\overrightarrow{PB}$,当直线l不垂直于x轴时,设直线l的方程,代入椭圆方程,由韦达定理,及函数的最值即可求得$\overrightarrow{PA}$?$\overrightarrow{PB}$的最小值,即可求得λ的最小值.
解答 解:(1)设椭圆的标准方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由2c=2,则c=1,
由2a=$\sqrt{2}$×2b,则a=$\sqrt{2}$b,①
由a2=b2+c2,即a2=b2+1,②
解得:a=$\sqrt{2}$,b=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)设A(x1,y1),B(x2,y2),
则$\overrightarrow{PA}$?$\overrightarrow{PB}$=(x1-2,y1)•(x2-2,y2)=(x1-2)(x2-2)+y1y2,
当直线l垂直于x轴时,x1=x2=-1,y1=-y2,且y12=$\frac{1}{2}$,
此时,$\overrightarrow{PA}$=(-3,y1),$\overrightarrow{PB}$=(-3,y2)=(-3,-y1),
∴$\overrightarrow{PA}$?$\overrightarrow{PB}$=(-3)2-y12=$\frac{17}{2}$,
当直线l不垂直于x轴时,设直线l:y=k(x+1),
由$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,消去y,整理得(1+2k2)x2+4k2x+2k2-2=0,
∴x1+x2=-$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$,
∴$\overrightarrow{PA}$?$\overrightarrow{PB}$=x1x2-2(x1+x2)+4+k2(x1+1)(x2+1),
=(1+k2)x1x2+(k2-2)(x1+x2)+4+k2,
=(1+k2)•$\frac{2{k}^{2}-2}{1+2{k}^{2}}$-(k2-2)•$\frac{4{k}^{2}}{1+2{k}^{2}}$+4+k2
=$\frac{17{k}^{2}+2}{2{k}^{2}+1}$=$\frac{17}{2}$-$\frac{13}{2(2{k}^{2}+1)}$<$\frac{17}{2}$,
要使不等式$\overrightarrow{PA}$?$\overrightarrow{PB}$≤λ(λ∈R)恒成立,
只需λ≥($\overrightarrow{PA}$?$\overrightarrow{PB}$)max=$\frac{17}{2}$,
∴λ的最小值为$\frac{17}{2}$.
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系,考查实数值的最小值的求法,解题时要认真审题,注意韦达定理、向量的数量积、椭圆性质的合理运用,属于中档题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值为20 | B. | 最小值为200 | C. | 最大值为20 | D. | 最大值为200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2018×22016 | B. | 2018×22015 | C. | 2017×22016 | D. | 2017×22015 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | C. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{4}-\frac{x^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
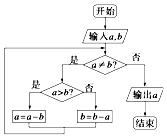 右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于2.
右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com